1's complement

In number representation techniques, the binary number system is the most used representation technique in digital electronics. The complement is used for representing the negative decimal number in binary form. Different types of complement are possible of the binary number, but 1's and 2's complements are mostly used for binary numbers. We can find the 1's complement of the binary number by simply inverting the given number. For example, 1's complement of binary number 1011001 is 0100110. We can find the 2's complement of the binary number by changing each bit(0 to 1 and 1 to 0) and adding 1 to the least significant bit. For example, 2's complement of binary number 1011001 is (0100110)+1=0100111.

For finding 1's complement of the binary number, we can implement the logic circuit also by using NOT gate. We use NOT gate for each bit of the binary number. So, if we want to implement the logic circuit for 5-bit 1's complement, five NOT gates will be used.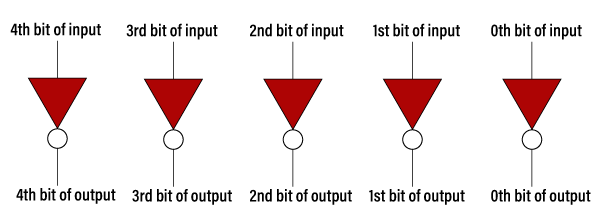

Example 1: 11010.1101

For finding 1's complement of the given number, change all 0's to 1 and all 1's to 0. So the 1's complement of the number 11010.1101 comes out 00101.0010.

Example 2: 100110.1001

For finding 1's complement of the given number, change all 0's to 1 and all 1's to 0. So, the 1's complement of the number 100110.1001 comes out 011001.0110.

1's Complement Table

Use of 1's complement

1's complement plays an important role in representing the signed binary numbers. The main use of 1's complement is to represent a signed binary number. Apart from this, it is also used to perform various arithmetic operations such as addition and subtraction.

In signed binary number representation, we can represent both positive and negative numbers. For representing the positive numbers, there is nothing to do. But for representing negative numbers, we have to use 1's complement technique. For representing the negative number, we first have to represent it with a positive sign, and then we find the 1's complement of it.

Let's take an example of a positive and negative number and see how these numbers are represented.

Example 1: +6 and -6

The number +6 is represented as same as the binary number. For representing both numbers, we will take the 5-bit register.

So the +6 is represented in the 5-bit register as 0 0110.

The -6 is represented in the 5-bit register in the following way:

1. +6=0 0110
2. Find the 1's complement of the number 0 0110, i.e., 1 1001. Here, MSB denotes that a number is a negative number.

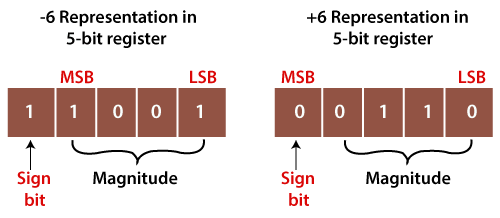
Here, MSB refers to Most Significant Bit, and LSB denotes the Least Significant Bit.

Example 2: +120 and -120

The number +120 is represented as same as the binary number. For representing both numbers, take the 8-bit register.

So the +120 is represented in the 8-bit register as 0 1111000.

The -120 is represented in the 8-bit register in the following way:

1. +120=0 1111000
2. Now, find the 1's complement of the number 0 1111000, i.e., 1 0000111. Here, the MSB denotes the number is the negative number.