8 Puzzle problems in Java

This puzzle contains the answers to the problems in the other 8 puzzles.

The player is given a 33-board with 8 tiles (each tile does have a number from 1 to 8) as well as a single vacant spot. To make the numbers on the tiles match the final arrangement, use the empty space to arrange them in a logical order. The allocated space can accommodate four neighbouring tiles (left, right, above, as well as significantly below).

One example is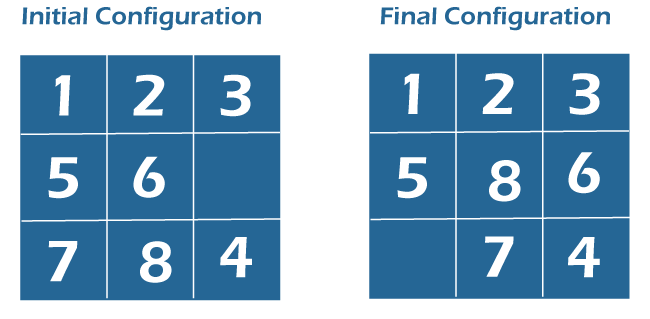

1. DFS (Brute-Force)

we can run a depth-first search on such a state-space tree, which is a collection of all possible solutions to a particular problem, or all possible states starting from the beginning state.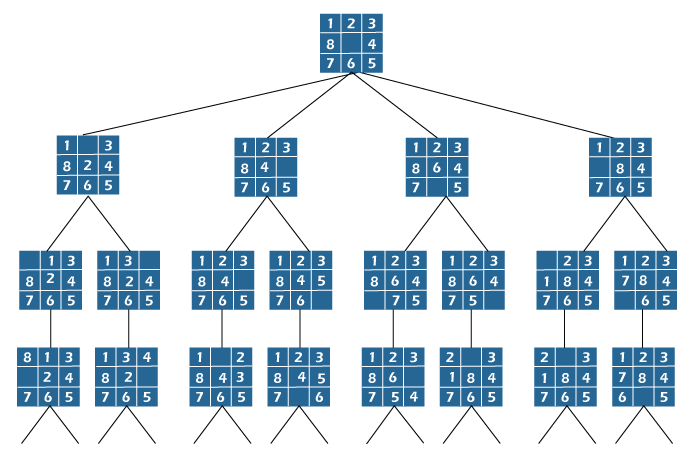

State Space Tree for 8 Puzzle

In this solution, subsequent moves might not always send us closer to the goal, but rather further away regardless of the original state, the state-space tree's search proceeds along the leftmost path starting at the root. An answer node may never be found using this approach.

2. A breadth-first strategy can be used to search the entire state space tree in BFS (Brute-Force). The closest goal state to the root is always found. No matter the beginning state, the algorithm nevertheless does the exact same set of steps as DFS.

3. Third, Branch and Bound An "intelligent" ranking function, sometimes known as that of an approximate cost function, could frequently accelerate the search for a single answer node by avoiding searching under sub-trees that do not contain an answer node. But it conducts a BFS-style search rather than using the backtracking technique.

Branch and Bound essentially entail three different types of nodes.

1. First live node A generated node that hasn't given birth to any offspring is said to be "living."
2. E-node At this time, research is being done on the offspring of the live E-node. Alternatively, an E-node appears to be a node that's also currently growing. Dead node
3. A dead node is a constructed node that won't be improved upon or further investigated. All of the children of a dead node have previously been extended.

Cost function:

The search tree's node X each has a cost attached to it. The cost function can be used to determine the following E-node. The following E-node has the lowest cost. The definition of the cost function is:

C(X) = g(X) + h(X) where

g(X) = cost of traveling to the current node from of the root

h(X) = cost of traveling from X to an answer node.

The best puzzle size is 8. Cost-based algorithm:

To move one tile in any direction, we assume this will cost one unit. As a result, we define the cost function as follows for an algorithm like the 8-puzzle method:

c(x) = f(x) + h(x) where

f(x) is the distance between the root and x in the path (the number of moves so far) and

h(x) is the quantity of non-blank tiles that are not in their desired positions (quantity of incorrectly positioned tiles). To change state x into a goal state, there have been at least h(x) moves required.

We have an algorithm for estimating the unknown value of h(x), which is available.

Complete Algorithm:

The path taken either by the aforementioned technique to go from the supplied initial configuration to the final configuration something like the 8-Puzzle is represented in the picture below. You should be aware that only the nodes also with the lowest cost function value were extended.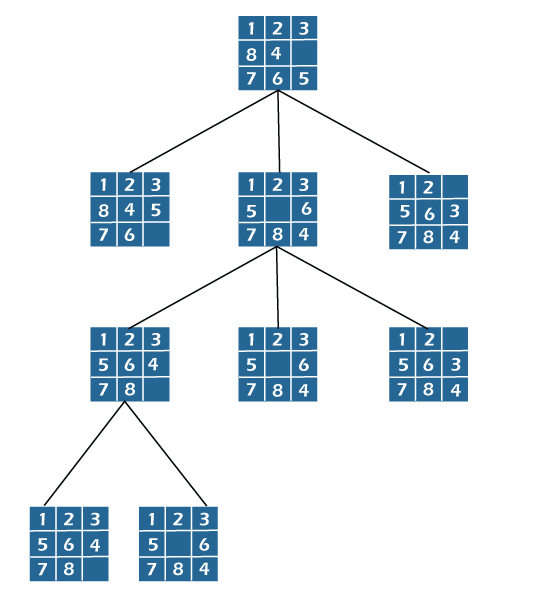

Program:

File name: PuzzleProblem.java

Output:

0 1 2 
4 5 8 
6 7 3 

0 1 2 
4 5 8 
6 7 3 

0 1 2 
4 7 5 
6 8 3 

0 1 2 
4 7 5 
8 6 3