What is the Full Form of ADC

ADC: Analog-to-Digital Converter

ADC stands for analog-to-digital converter. It (ADC, A/D, or A-to-D Converter) is a device primarily used to convert the signal; it first takes an Analog signal and then turns it into a digital format. AD converters are used for different purposes, and they are used in a variety of applications, such as digital music, radio, and digital photography. It is also used for digital signal processing.

The concept that is used in ADC is quite simple. The working of ADC is very straightforward; it takes an Analog signal and then converts it into digital format. It transforms an Analog signal of various forms, such as sound or electricity, into a digital representation. These ADC devices receive and store data using billions of small binary digits.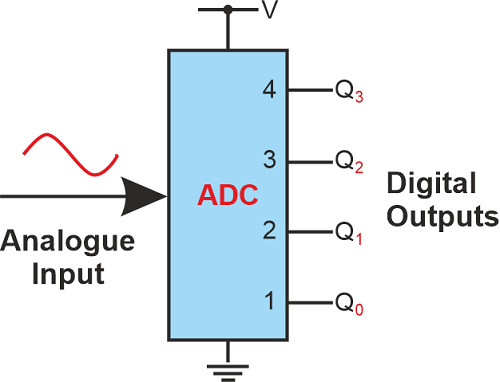

Nowadays, Analog to digital converter is used in several technologies and electronic devices like computers, mobile phones and many others. Analog-to-digital converters are mainly used to convert the incoming signals that come from the physical world and are frequently converted via ADC converters into the binary format (mainly in zero and one form) of computers. Signals like sound and electricity may have infinite shapes and forms when they are in their Analog state. ADC may be applied to process them and modify them in an almost alternative manner.

Working of the ADC

Analog to digital converter is considered a beneficial component when dealing with digital systems because it communicates with real-time signals. These digital systems must interpret real-world/time signals to correctly give crucial information. For instance, IoT develops fast applications and devices in daily life with the help of ADCs. We will now go into the theory and operation of ADCs.

In the real world, Analog signals are mainly those signals that have a chaining sequence with a constant value (though there are certain cases in which it can be limited). These types of signals are acquired from various sources; they can come as sound, light, temperature and motion. Digital signals are mainly represented with the help of a sequence of discrete values. The way that discrete values are used to describe digital signals depends on the time series or sampling rate at which the signals are divided into sequences (more on later).

The simplest way to explain this is through an easy diagram. An excellent representation of both Analog and digital signals may be seen in the following image, where the red line represents the Analog input signals while the green line represents the digital output signals.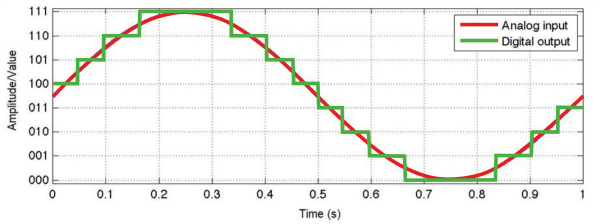

What is the ADC sampling rate?

The Analog to digital converter sampling rate is also known as the sampling frequency and the rate of sampling of an ADC. It can be related to speed. The sampling rate is calculated using a formula in which the units are measured in SPS (sample per second) or S/s (otherwise, if you use the sampling frequency, it would be in Hz). One of the best things about ADC is that the more significant number of samples it takes, the higher the frequency it returns.

With the formula, the sampling frequency or sampling rate, fs, can be easily calculated, which refers to the average number of samples obtained in one second.

The one important equation that is used for measuring the sample rate is denoted below:

fs = 1/T

Where fs stands for the sample rate/frequency, and T stands for the sample period or the time it is used for sampling. For instance, it appears that if fs is 20 S/s (or 20 Hz) and T is 50 ms (millisecond). Despite the prolonged sample rate, the signal will still resemble the Analog signal it was designed for. This is mainly due to the frequency of the original signal being less than 1 Hz, suggesting that the frequency rate was still high enough to recreate the call with the same frequency.