ALU and Data Path in Computer Organization

Earlier, representing and storing numbers were the basic operation of computers. But when computers came with computation, manipulating numbers like adding, multiplying operations, then these operations are handled by the computer's ALU or arithmetic logic unit.

The central processing unit (CPU) can be divided into two sections:

Data section: Memory, registers, adders, ALU, and communication buses. Each step (fetch, decode, execute, save the result) requires communication (data transfer) paths between memory, registers and ALU. It is also known as the data path.
Control section: Data path for each step is set up by control signals that set up dataflow directions on communication buses and select ALU and memory functions. Control signals are generated by a control unit consisting of one or more finite state machines.

Data Path

Suppose any data processing operation should be performed in the CPU like transferring the content of register from one place to another, from one register to another register, performing the addition of two numbers in ALU, copying something in memory and copying to register. So, any data processing operation happens in the CPU, and then for that data operation, data follows a specific path, called "data path".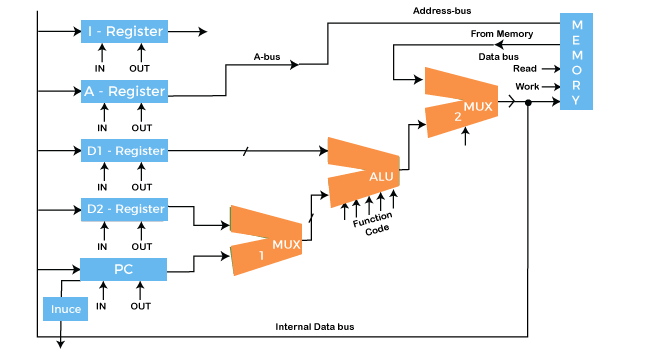

A data path is a collection of functional units such as arithmetic logic units or multipliers that perform data processing operations, registers, and buses. Along with the control unit, it composes the central processing unit (CPU). A larger data path can be made by joining more than one data path using multiplexers.

A data path is the ALU, the set of registers, and the CPU's internal buses that allow data to flow between them.

The simplest design for CPU uses one common internal bus, and efficient addition requires a slightly more complicated three-internal-bus structure. Many relatively simple CPUs have a 2-read, 1-write register file connected to the 2 inputs and 1 output of the ALU.

1. Arithmetic Logic Unit (ALU)

The ALU is the mathematical brain of a computer. The ALU is a digital circuit that provides arithmetic and logic operations. It is the fundamental building block of the central processing unit of a computer. It is present in every CPU to perform operations like addition, subtraction, division, multiplication and many more.

It is the main component of the system to apply logic to execute a particular instruction or program. ALU takes two operands as input and function code, and ALU can perform multiple functions like subtraction, X-NOR, division and many more.

In addition to ALU modern CPU contains a control unit and a set of registers. Most of the operations are performed by one or more ALU's, which load data from the input register. Registers are a small amount of storage available to the CPU, and these registers can be accessed very fast. The control unit tells ALU what operation to perform on the available data. After calculation or manipulation, the ALU stores the output in an output register.

2. Registers

Registers are like gates here through which signals are further sent to components to do the micro-operation. Registers are controlled, and signals of registers are directed by the control- unit. Here are five registers used to store in-out signal data:

Program Counter
The program counter (PC) is a CPU register in the computer processor which has the address of the next instruction to be executed from memory. As each instruction gets fetched, the program counter increases its stored value by 1. It is a digital counter needed for faster execution of tasks and tracking the current execution point.
Instruction Register
In computing, an instruction register (IR) is the part of a CPU's control unit that holds the instruction currently being executed or decoded. An instruction register is the part of a CPU's control unit that holds the instruction currently being executed or decoded. The instruction register specifically holds the instruction and provides it to the instruction decoder circuit.
Memory Address Register
The Memory Address Register (MAR) is the CPU register that either store the memory address from which data will fetch from the CPU or the address to which data will be sent and stored. It is a temporary storage component in the CPU (central processing unit) that temporarily stores the address (location) of the data sent by the memory unit until the instruction for the particular data is executed.
Memory Data Register
The memory data register (MDR) is the register in a computer's processor, or central processing unit, CPU, that stores the data being transferred to and from the immediate access storage. Memory data register (MDR) is also known as memory buffer register (MBR).
General Purpose Register
General-purpose registers are used to store temporary data within the microprocessor, and it is a multipurpose register. They can be used either by a programmer or by a user.

3. BUS

In early computers, the bus was parallel electrical wires with multiple hardware connections. Therefore a bus is a communication system that transfers data between components inside a computer or between computers. It includes hardware components like wires, optical fibers, etc. and software, including communication protocols.

The Registers, ALU, and the interconnecting BUS are collectively referred to as data paths. Here are the following types of the bus, such as:

Address bus: The buses which are used to carry address.
Data bus: The buses which are used to carry data.
Control bus: If the bus is carrying control signals.
Power bus: If it is carrying clock pulse, power signals, it is known as a power bus.

The bus can be used for a single purpose or multiple purposes. When we would have different kinds of buses, different types of bus organizations will take place, such as:

One Bus organization

In one bus organization, a single bus is used for multiple purposes. A set of general-purpose registers, program counters, instruction registers, memory address registers (MAR), and memory data registers (MDR) are connected with the single bus. Memory read/write can be done with MAR and MDR.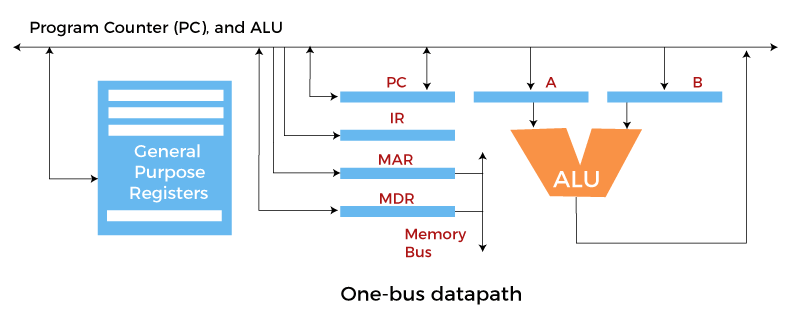

The program counterpoints to the memory location from where the next instruction is to be fetched. The instruction register will hold a copy of the current instruction. In one bus organization, only one operand can be read from the bus at a time.

If the requirement is to read two operands for the operation, then the read operation needs to be carried twice. So that's why it is making the process a little longer. One of the advantages of one bus organization is that it is one of the simplest and also this is very cheap to implement.

At the same time, there is a disadvantage that it has only one bus. This "one bus" is accessed by all general-purpose registers, program counter, instruction register, MAR, and MDR, making every operation sequential. No one recommends this architecture nowadays.

Two Bus organizations

This overcame the disadvantage of one bus organization, and another architecture was developed known as two bus organization. In two bus organizations, there are two buses, and the general-purpose register can read/write from both the buses. In this case, two operands can be fetched at the same time because of the two buses.

One bus fetch operand for ALU and another bus fetch for register. The situation arises when both buses are busy fetching operands, the output can be stored in a temporary register. When the buses are free, then the particular output can be dropped on the buses.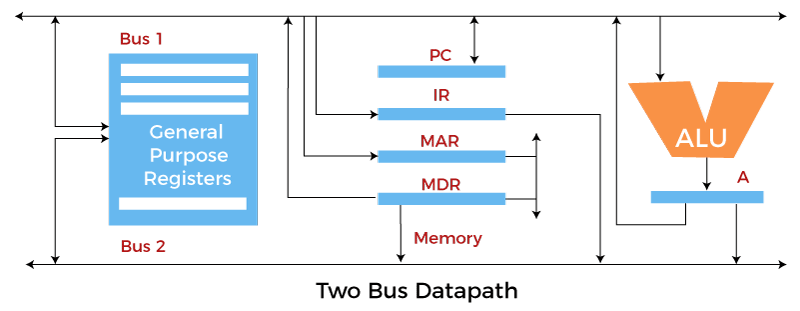

There are two versions of two bus organizations, i.e., in-bus and out-bus. From in-bus, the general-purpose register can read data, and to the out bus, the general-purpose registers can write data. Here buses get dedicated.

Three Bus organization

In three bus organizations, we have three buses, OUT bus1, OUT bus2, and an IN bus. From the out buses, we can get the operand that can come from the general-purpose register and evaluated in ALU, and the output is dropped on In Bus to be sent to respective registers.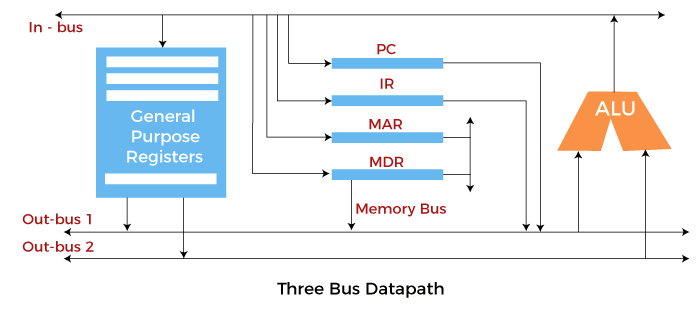

This implementation is complex but faster because two operands can flow into ALU and out of ALU in parallel. It was developed to overcome the "busy waiting" problem of two bus organizations.

In this structure, after execution, the output can be dropped on the bus without waiting because of an extra bus. The main advantages of multiple bus organizations over the single bus are: