Angle of a circleAn angle is formed between the intersections of two lines. The angle of a circle or the central angle is the angle formed between the two radii, tangents, or chords. A radii is the radius of the circle. A tangent is a straight line touching or intersecting the circle at a specific point. It does not pass through the center of the circle. A chord is a line joining any two points on a circle. Angle is represented by the symbol theta (θ). Here, we will discuss the following:
Central angleThe central angle is the angle formed between the two radii in a circle. The vertex of the central angle lies at the center of the circle. 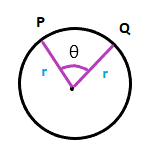
Where, r is the radius of the circle θ is the central angle PQ is the length of the arc of the circle Any line passing through the center of the circle is known as diameter of the circle. 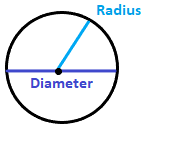
Radius = Diameter/2 Or Diameter = 2Radius Length of arc = 2πr × (θ/360) θ = 360L/2πr Where, r is the radius of the circle θ is the angle in degrees. π is equal to 3.1415 or 22/7. L is the length of the arc Thus, Central Angle θ = 360 x L/2πr Central angle in radians is given by: L = r θ θ = L/r Where, r is the radius of the circle θ is the angle in radians. L = Arc length ExamplesLet's discuss two examples based on the central angle of a circle. Example 1: Find the central angle of a circle with a radius 5m and length of the arc is 12m. Solution: Radius of the circle = 5m Length of the arc = 12m Central Angle θ = 360 x L/2πr θ = 360 x 12/2π5 θ = 137.5 Thus, the central angle of the circle with a radius 5m and arc length of 2m is 137.5 degrees. Example 2: Find the arc length of a circle with central angle and radius of 4 radians and 2 cm. Solution: θ = L/r L = θr L = 4 x 2 L = 8m Thus, the length of the arc is 8 cm. Example 3: Find the central angle of a circle with radius 4 cm and arc length 0.16m. Solution: Radius of the circle = 8 cm Length of the arc = 0.16m To find the central angle, we need to convert the different units of the radius and length to the same unit. Length of the arc = 0.16 x 100 = 16cm 1m = 100 cm Central Angle θ = 360 x L/2πr θ = 360 x 16/2π8 θ = 114.6 Thus, the central angle of the circle with a radius 8cm and arc length of 0.16m is 114.6 degrees. Example 4: Find the central angle in radians with a radius 6 m and arc length of 12 m. Solution: θ = L/r θ = 12/6 θ = 2 Thus, the central angle of a circle is 2 radians. Interior angleThe angle formed inside a circle is known as the interior angle of a circle. The vertex of the interior angle lies anywhere inside the circle or on the arc. Thus, the angle formed between the intersections of two lines inside a circle is the interior angle of a circle. For example, 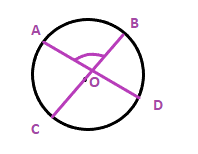
Angle AOB is the interior angle of the circle. ExamplesExample 1: Find the interior angle RPQ in a circle with radius 15cm and an angle of 80 degrees? 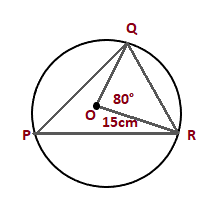
Solution: OR = 15cm According to the angle theorem, the angle RPQ is half the angle ROQ. RPQ = ½ x 80 RPQ = 40 degrees Thus, the value of angle is RPQ is 40 degrees. Example 2: Find the interior angle AOB and angle COD in the below diagram. 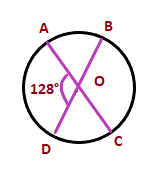
Solution: BOD is a straight line. The line OA intersects the line in two parts. Angle AOD + Angle AOB = 180 ° 128° + Angle AOB = 180 ° Angle AOB = 180 - 128 Angle AOB = 52° Angle COD is the opposite angle of AOB. According to the angle theorem, the opposite angles are equal. Thus, Angle COD = 52° Exterior angleThe angle formed outside a circle is known as the interior angle of a circle. The vertex of the interior angle lies anywhere outside the circle or on the arc. Thus, the angle formed between the intersections of two lines outside a circle is the interior angle of a circle. For example, 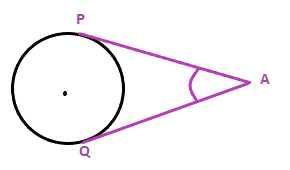
Angle PAQ is the exterior angle of the circle. ExamplesExample 1: Find the angle PAQ? 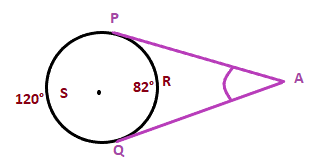
Solution: Given: Angle PSQ = 120° Angle PRQ = 82° According to the angle theorem, Angle PAQ = ½ (Angle PSQ - Angle PRQ) Angle PAQ = ½ (120 - 82) Angle PAQ = ½ (38) Angle PAQ = 19° Thus, the exterior angle PAQ is equal to 19 degrees. Example 2: Find the value of angle X? 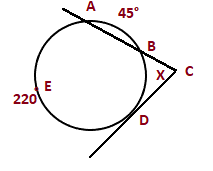
Solution: The circle has three intercepts with has three angle values. 220 + 45 + BD = 360 BD = 360 - 265 BD = 95 According to the angle theorem, Angle X = ½ (Angle AED - Angle BD) Angle X = ½ (220 - 95) Angle X = ½ (125) Angle X = 62.5° Thus, the value of angle X is 62.5 degrees. An interior angle is formed inside the circle, while the exterior angle is formed outside the circle.
Next TopicNumber Names from 1 to 100
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










