Applications of Tree in Discrete Mathematics

Trees

A Tree can be described as a collection of nodes, known as a graph with connecting lines or edges between the nodes. So we can say that lines are used to connect all the nodes. The first node of the tree is known as the root.

The various application of tree is described as follows:

Binary Search Tree

The most important task is searching for items in a list. Our main goal is to efficiently search the items when they are ordered by implementing the search algorithm. We can use the binary search tree so that we can accomplish it. In the binary search tree, each child of the vertex is divided into the right child or subtree or left child or subtree. Both the subtree of a vertex (left or right child) can only be one. Every vertex of a tree has a value known as a key. The left subtree of a vertex is used to contain various vertices with keys, but this key must be less than the key of vertex. The right subtree of a vertex is used to contain various vertices with keys, but this key must be greater than the key of vertex. The right subtree and left subtree should be a binary search tree.

Method of insertion in Binary tree

In the starting, the tree contains only one vertex, which is called root. After that, we will assign the first item, which is known as the key of root.

For example: Suppose we want to insert 45. Then 45 will become the root of this tree, which is described as follows:

If we want to insert items in the tree first, we have to compare it with the key of root. If it is less than the key, it will move to the left and will be known as the left child otherwise, it will move to the right and will be known as the right child. The left child and right child of a root cannot be more than one.

For example:

• Suppose the root is 45, and we want to insert 39 and 50. In this case, first, 39 will be compared with 45. Item 39 is less than 45, so it will be added to the left of 45. Item 39 will be known as the left child of root 45.
• After that, we will insert 50. We will also compare it with 45. Item 50 is greater than 45, so it will be added to the right of 45. Item 50 will be known as the right child of root 45.

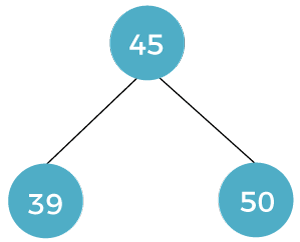
If we want to insert more items, we have to follow the above procedure. That means we will first compare items with the root. According to this comparison, we will compare it with the left or right child. If the new item is less than the left child, it will move to the left of this left child otherwise, it will move to the right of this left child. Otherwise, we will compare the new item with the right child. If the new item is greater than the right child, it will move to the right of this right child otherwise, it will move to the left of this right child.

For example:

• In the above tree, suppose we want to insert 33, 41, 47, and 52. In this case first, we have to follow the above procedure. So we will first try to insert 33. For this, we will compare 33 with 45. It is less than 45, so it will move to the left. Now we will compare 33 with 39. It is less than 39, so it will move to the left, and 33 will add there.
• Now we will insert 41. So we will compare it with 45. It is less than 45, so it will move to the left. Now we will compare it with 39. It is greater than 39, so it will move to the right, and 41 will add there.
• After that, we will insert 47. So we will compare 47 with 45. It is greater than 45, so it will move to the right. Now we will compare 47 with 50. It is less than 50, so it will move to the left of 50, and 47 will add there.
• Now we will insert 52. So we will compare 52 with 45. It is greater than 45, so it will move to the right. Now we will compare 52 with 50. It is greater than 50, so it will move to the right of 50, and 52 will add there.

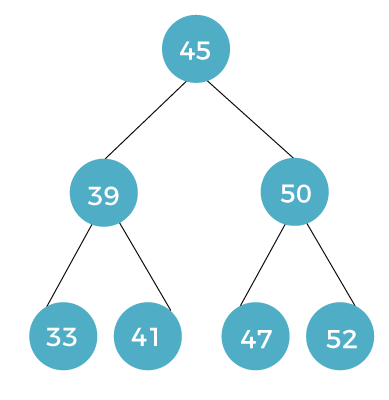
There can be another case in which the left or right sub-child can also have more than one child. In this case, we have to compare all the items of last node, and according to their comparison, put it on the left or right side.

For example:

• In the above tree, suppose we want to insert 31, 35, 37, 40, 44, 46, 48, 51, and 55. In this case, first we have to follow the above procedure. So first, we will try to insert 31. For this, we will compare 31 with 45. It is less than 45, so it will move to the left. Now we will compare 31 with 39. It is less than 39, so it will move to the left and again compare with 33. It is less than 33, so 31 will add on the left of 33.
• Now we will try to insert 35. So we will compare it with 45. It is less than 45, so it will move to the left. Now we will compare it with 39. It is less than 39, so 35 will move to the left and again compare with 33. Item 35 is greater than 33, so it will move to the right.
• Now we will try to insert 37. So we will compare it with 45. It is less than 39, so it will move to the left and again compare with 33. It is greater than 33, so it will move to the right, but 33 is already has a right child 35. So we have to again compare 37 with 35. It is greater than 35, so 37 will add after 35.
• The same procedure will be followed to insert all the remaining items. So 40 will be added on the left side of 41, and 44 will be added on the right side of 41. When we try to insert 46 and 48, then 46 will be inserted on the left side of 47, and 48 will be inserted on the right side of 47. Finally, if we try to insert 51 and 55, then 51 will be inserted on the left side of 52, and 55 will be inserted on the right side of 52.

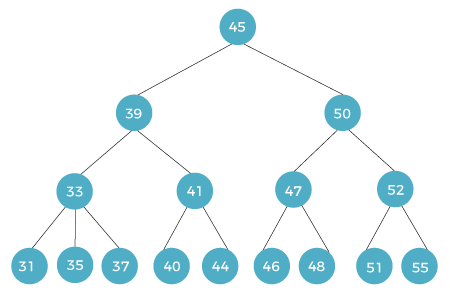
Algorithm of Insertion of Binary search tree

Step 1: START

Step 2: Store the key to be inserted (x)

Step 3: Check element present in tree if not go to step 4 else step 5

Step 4: Make inserted key Root Node

Step 5: Compare x with root node if smaller go to step 6 else go to step 7, or no root node find goto step 9.

Step 6: Element reaches the left subtree repeat Step 5

Step 7: Element reaches the right subtree repeat Step 5

Step 8: Insert the key

Step 9: STOP

Decision Tree

The decision tree is a hierarchical tree structure or a diagram, which helps us to choose between various actions. It is mostly used for decision-making purposes. It is a type of rooted tree in which each internal vertex corresponds to a decision. These vertices contain a subtree for each possible outcome of the decision. The paths to leaves vertex correspond to the possible solutions to the problem. A decision tree contains a tree-like structure that's why people can easily understand the logic behind this tree. Using this tree, people can easily make their decision because it split our problems into smaller parts, which helps us to take our decision very easily.

On the basis of the attribute value test, the decision tree spits the subset into the smaller subset. In a recursive manner, we will repeat this process on each derived subset. This process is known as recursive partitioning. When the target variable and the subset at a node all have the same value, then the process of recursion will be completed. If we are unaware that how to construct the decision tree classifier, then we don't need any parameter setting or domain knowledge for this. The high-dimensional data can be easily handled by the decision tree. The accuracy of decision tree classifier is very nice.

Representation of Decision tree

In the decision tree, we will classify the instance by sorting them down the tree. We will sort them from the root to some leaf node, and these leaf nodes are used to provide the classification of the instance. To classify the instance, we will start from the tree's root node. Then we will test the attributes, which are specified by this node. After that, we will move down to the tree branch, which corresponds to the attribute's value. We will repeat this process for the subtree, which is rooted at the new node.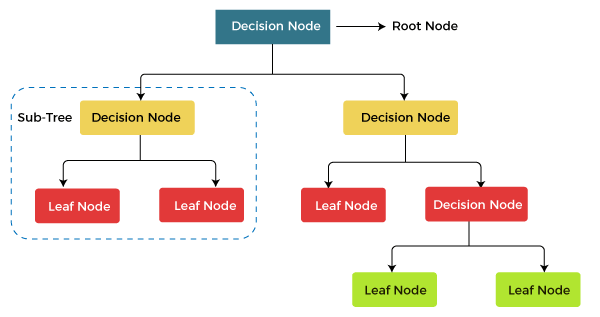

Example of decision tree

Suppose we have an offer letter. Now we have to decide whether we will accept this letter or not.

Solution:

For this problem, we will create a decision tree, which begins with the root node that is the Salary attribute. Now our root node will split into two nodes: a decision node, which will be used to show the distance between home and office, and a leaf node, which will be created on the basis of corresponding labels. After that, the next decision node will again split into two nodes: a decision node, which will be used to show the Cab facility, and a leaf node. Finally, the decision node will split into two leaf nodes: one is for Accepted offers, and another is for Declined offers.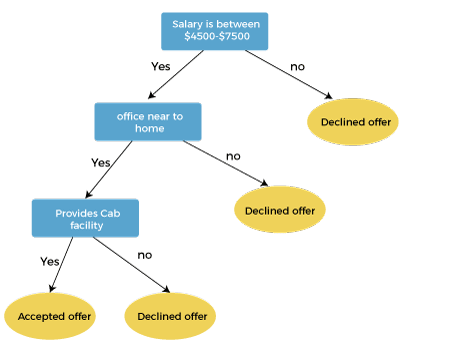

Game Tree

The game tree can be described as a type of recursive search function, which is used to examine all possible moves of the strategy game. It will also examine the results so that they can ascertain the optimal moves. If the artificial intelligence has a scenario in which they have less number of possible choices per play and don't need real-time decision making, in this case, the game tree will be very useful for them. Generally, the game tree is used to find out the best possible move in a board game. To explain the game tree, we will use the tic-tac-toe game as an example, which is described as follows: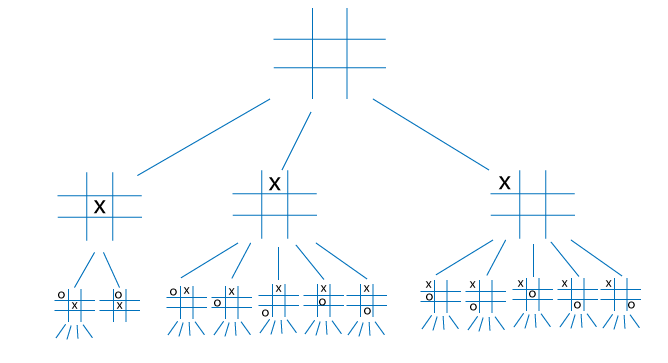

So we will start from the current board position. Now we have to check all possible moves made by the computer. Using these all possible moves, we will check that what moves the other player may make. After that, we will look at the computer. Now the computer will flip back and make moves for the other player and itself. The computer continuously makes the moves until the game is completed. For every possible outcome, the computer will do this, and it plays thousands of games. Lastly, it finds out the best chance of success by looking at the outcome of losers and winners of these games. If the game which we are playing has no end, the game tree will go to infinite.

In the game tree, we check every possible move and also every move of the opponent. After that, we will try to see that after how many moves they are winning. In the world, we have a huge amount of possible games. In our example, we use a tic-tac-toe game. In this game, the first move contains 9 possible moves. In the second turn, it will reduce to 8, then 7, 6, etc. So in this game, there are total 255,168 possible moves. In the game tree, the main goal is to see all these moves and choose a move that has all the chances of winning this game.

Working of Computer on Game Tree

The computer examines all possible moves and starts evaluating a move that has a high possibility of winning the game. The tic-tac-toe game has a grid that contains a lot of empty squares. The computer can fill any of the empty squares. So we can say that number of empty squares and the number of possible moves are the same. When they found all these moves, they will create a loop over each possible move and then try to determine that whether the move will result in a win or not.

We will extend the game tree into branches to determine that the move is good or bad. We will extend the tree until the game is completed or until the terminal node. The last node of the tree is known as the terminal node. On the basis of the game's result, the value of terminal node is assigned. If the terminal has a higher value, then the result will be very good for the computer because they have only two possible results that are win or loss. The result of the games can be represented by the value of -1 and 1. The terminal node uses the rules of game and displays the payoff value for max calculation. The pictorial representation of terminal node, computer move and opponent move is described as follows:

In the following image, we can see that the values of terminal node have been determined by the nodes D, E, F, and G. To find the other node's payoff value, a minimax algorithm will be used. The node will be shown Max if the node shows the moves of computer's choice. The node will be shown Min if the node shows the moves of player's choice. The max node's value becomes that the highest node beneath it and the same as for the min node.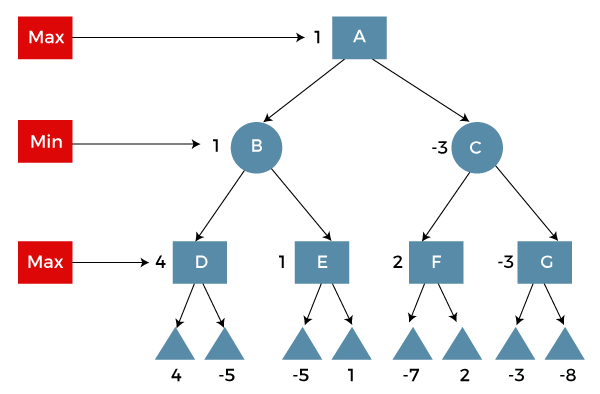

In this example, the D's value is 4, and E's value is 1. The B's value becomes 1, which is the lowest of 4 and 1. If we move up in this image, we will see that each node has a value. We will assume that the top node A has the highest or maximum value of the nodes beneath it. The highest value node shows the move, which should be made by the computer. If the game wins by the opponent, the position will be known as a winning position for the opponent. In this case, the move of the computer will be called as a bad move. If the game wins by the computer, the position will be known as a winning position for the computer. In this case, the move of the opponent will be called as a bad move.