Aptitude Height and Distance Test Paper 26) The angle of elevation of the sun when the length of the shadow of a pole is equal to the height of the pole is?
The Correctoption is(A) Answer with explanation: 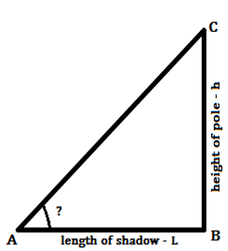
Let ∠BAC = θ Let height of pole is h and length of the shadow is L. As per question L = h 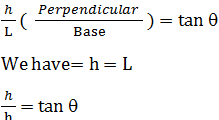
tan θ = 1 So, when tan θ is equal to 1 the angle will be 45° (Option A) 7) A man sees the top of a tower from a point P. It makes an angle of elevation of 30° with the man's eyes. If the height of the tower is 100 m, find the distance between man and tower?
The Correctoption is(C) Answer with explanation: 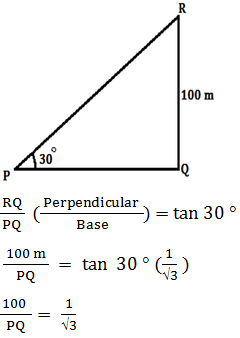
PQ = 100 * √3 PQ = 100 * 1.73 = 173 m (Option C) 8) A storm breaks a tree. The broken part of tree bends so that the top of the tree touches the ground and makes an angle of 60° with the horizontal plane. If the distance between the base of the tree and the point where top of tree touches the ground is 10 m, find the height of the tree?
The Correctoption is(A) Answer with explanation: 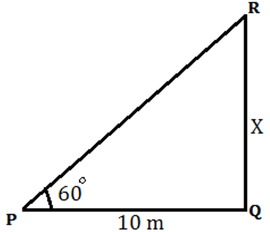
PQ = 10 and let RQ be X. 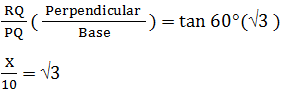
X = 10 √3 Now, PR2 = X2 + (10)2 PR2 = (10 √3)2 + (10)2 = 300 + 100 PR2 = 400 PR = 20 Height of tree = RQ + PR = X + 20 = 10 √3 + 20 = 10 * 1.73 + 20 = 17.3 + 20 = 37.3 meter (Option A) 9) The angle of elevation of the top of an unfinished building at point P which is 120 m away from its base is 30°. If the angle of elevation of the finished building at the same point would be 60°, find the height of the remaining part of the building.
The Correct option is(C) Answer with explanation: 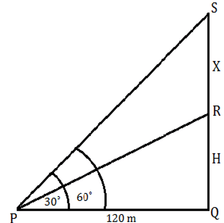
Let the height of remaining part of building be X. then, 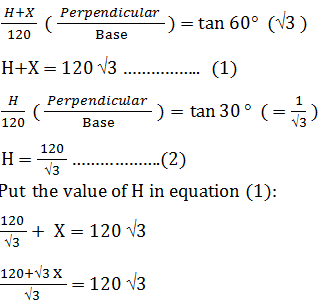
120 + √3 X = 120*3 120 + √3 X = 360 √3 X = 360 - 120 √3 X = 240 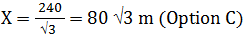
10) The top of a 30 m high wall makes an angle of elevation of 60° with the top of a tower and makes an angle of depression of 45° with the bottom of the tower. Find the distance between tower and wall?
The Correctoption is(D) Answer with explanation: 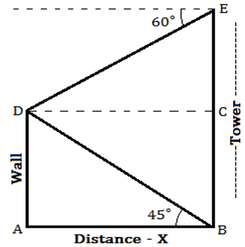
Let AD is the wall of height 30 m and BE is the tower and X be the distance between tower and wall. 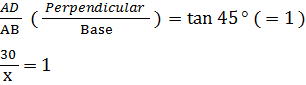
X = 30 m (Option D)
Height and Distance Aptitude Test Paper 1
Height and Distance Aptitude Test Paper 3 Height and Distance Aptitude Test Paper 4 |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










