Aptitude Logarithm Test Paper 11) Find the logarithm of 1/256 to the base 2√2.
Answer: C Explanation: Let log2√2 [1/256] = x We know that loga y = x is similar to ax = y So, we can write it as [1/256] = (2√2) x Or, (2√2) x = [1/28] Or, [21 * 21/2]x = 1/28 Or, 23x/2 = 2-8 Therefore, 3x/2 = -8 Hence, x = (-8 * 2)/ 3 = -16/3 2) If loga [1/36] = -2/3, find the value of a.
Answer: D Explanation: ATQ, loga [1/36] = -2/3 We know that loga y = x is similar to ax = y So, a (-2/3) = 1/36 Or, a (-2/3) = 1/62 Or, a (-2/3) = 6-2 Now, multiply and divide by 3 in the power of 6 to make the power equals to power of a. So, a (-2/3) = 63(-2/3) On comparing both side, we get a = 63 Therefore, a = 216 3) Find the value of x Log4(log8 64) = log5 x
Answer: D Explanation: ATQ, Log4 (log8 64) = log5 x...... (i) Let, log8 64 = a Or, 64 = 8a, or 8a = 82 That means a=2 Now, put log8 64 = 2in equation 1. Log4 (2) = log5 x...... (ii) Now, let log4 2 = s Or, 4s = 2, or 22S = 2 Now, on comparing both side we get 2s = 1, or s = ½ Put the value of s in equation 2 So, log5 x = ½ Therefore, x = 51/2 = √5 4) The equation, a2 + b2 = 7ab equals to
Answer: A Explanation: Here, a2 + b2 = 7ab Add both sides 2ab to make a formula. Or, a2 + b2 + 2ab = 7ab + 2ab Or, (a+b) 2 = 9ab Or, (a+b) 2 / 9 = ab Or, [1/3 (a+b)]2 = ab Now, taking log both sides Therefore, log [1/3 (a+b)]2 = log ab We know that log m*n = log m + log n, and log mn = n log m So, 2 log [1/3 (a+b)] = log a + log b Therefore, log [1/3 (a+b)] = 1/2(log a + log b) = a2 + b2 = 7ab 5) If (log3 x)(logx 2x)(log2x y) = logx x2, find y.
Answer: A Explanation: (log3 x)(logx 2x)(log2x y) = logx x2 B = C = Now, ATQ, A* B * C = logx x2 We know that, loga mn = n loga m We know that loga a = 1 Aptitude Logarithm Test Paper 2 Aptitude Logarithm Test Paper 3 Aptitude Logarithm Test Paper 4
Next TopicAptitude Logarithm Test Paper 2
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





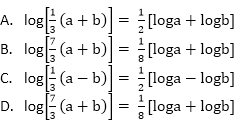
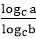
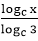
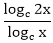
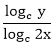
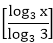 *
*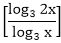 *
* 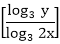 =
= 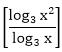
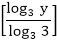 =
=