|
6) Out of 7 constants and 4 vowels, how many words of 3 constants and 2 vowels can be formed?
Answer: B Answer with the explanation: We can combine 3 consonants and 2 vowels out of 7 consonants and 4 vowels in a way 7C3 * 4C2 = That means 210 groups having 3 consonants and 2 vowels. Each group consists of 5 words that mean the possible arrangement of the letters is 5! Or, 5! = 5*4*3*2*1 = 120 ways. Therefore, the required number of words = 210*120 = 25200. 7) How much 4-digit number can be formed from the digits 2, 3, 4, 5, 6, and 7 which are divisible by 5 in such a way that digits should not repeat.
Answer: D Answer with the explanation: A number is divisible by 5 if the number ends with 0 or 5, but we don't have 0 in the given digits that means 5 should come at the unit place. Now, one of the remaining 5 digits (2, 3, 4, 6, and 7) can come at the tens place. 8) In what ways the letters of the word "CRICKET" can be arranged to form the different new words so that the vowels always come together?
Answer: A Answer with the explanation: The word CRICKET has 7 different letters, but ATQ, the vowels should always come together. Note: Here 2! is taken in the denominator, because the letter C is repeated twice.Now, the vowels IE can be arranged in 2 different ways, i.e., 2P2 = 2! = 2*1 = 2 ways. So, the new words that can be formed = 60*2 = 120. 9) In what ways the letters of the word ?MACHINE? can be arranged so that the vowels occupy only the odd positions?
Answer: C Answer with the explanation: The word machine consists of 7 letters in which there are 3 vowels and 4 consonants. Similarly, the number of ways to arrange the consonants = 4P4 = Note: we know that 0! = 1Therefore the required numbers of ways = 24*24 = 576 10) In what ways the letters of the word ?ACTORS? can arrange so that the vowels occupy only the even positions?
Answer: B Answer with the explanation: The word ACTORS consist of 6 letters in which there are 2 vowels and 4 consonants Similarly, the number of ways to arrange the consonants = 4P4 = Note: we know that 0! = 1Therefore the required numbers of ways = 6*24 = 144 Permutation and Combination Test Paper 1 Permutation and Combination Concepts
Next TopicPermutation and Combination Concepts
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





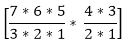 = 210
= 210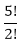 =
= 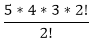 = 5*4*3= 60 ways.
= 5*4*3= 60 ways.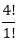 =
= 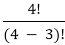 = 4*3*2*1 = 24
= 4*3*2*1 = 24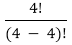 = 4*3*2*1 = 24
= 4*3*2*1 = 24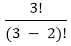 =
= 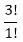 = 3*2 = 6 ways
= 3*2 = 6 ways 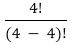 = 4*3*2*1 = 24 ways
= 4*3*2*1 = 24 ways




