Speed Time and Distance Test Paper 3

The Correct answer is (D)

Answer with explanation:

The bus covers a distance of 60 km in an hour if it stops at the bus stops.

The bus covers a distance of 65 km in an hour if it does not stop at the bus stops.

Due to stoppages it covers 5 km less.

If it does not stop it will cover 5 km more.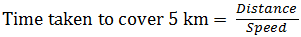

Time =⁵⁄₆₅→¹⁄₁₅hour

We need answer in minutes so ¹⁄₁₅* 60=4 minutes (Option D)

The Correct answer is (C)

Answer with explanation:

The total distance between the bus stations is 200 km. So, when the buses cross each other the sum of the distances travelled the buses will be equal to 200 km.

We have given that buses cross each other at a distance of 120 km from one of the stations. So one bus covers a distance of 120 km and the other bus covers the rest of the distance (200-120=80km).

The ratio of their speeds will be equal to the ratio of distances covered by them.

So, ratio of speeds = ¹²⁰⁄₈₀→³⁄₂(Option C)

The Correct answer is (B)

Answer with explanation:

Let the time taken to complete the first half of the journey = X hour

∴ the time taken to complete the second half of the journey = (5 - X)

Distance covered in first half = Distance covered in second half

Distance covered in first half = speed * time→20*X=20X

Distance covered in second half = speed * time→25 * (5-X)

So, 20X = 25 * (5-X)

20X = 125 -25X

45X = 125

X= ¹²⁵⁄₄₅= 2.7 km

X is the distance covered in first half which is equal to the distance covered in the second half.

So to get the total journey we will multiply X with 2.

Total journey in Km = 2.7 x 2 = 5.4 km (Option B)

The Correct answer is (C)

Answer with explanation:

Let the actual distance travelled by man = X km

In this problem, time is same for both the situations when the man runs at 20 km/hr and 24 km/hr.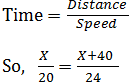

24X = 20X + 800

4X = 800

X =⁸⁰⁰⁄₄= 200 km (Option C)

The Correct answer is (D)

Answer with explanation:

Let the speed of the car = X km/hr

∴ the speed of the bus will be = X *¹⁵⁰⁄₁₀₀=³⁄₂X

Both bus and car take equal time to reach the station Q.

The bus stops for 10 minutes at the bus stop. So if the bus would not have stopped it would have reached the station Q, 10 minutes earlier and the difference between the time taken by the car and bus would have been = 10 minutes or¹⁰⁄₆₀ hours.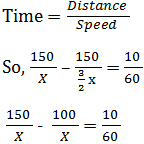

3000 = 10 X

X =³⁰⁰⁰⁄₁₀= 300 km/hr (Option D)