Aptitude Square Roots and Cube Roots Concepts and FormulasPoints to Remember:1) If a2 = b, we say that square root of b is "a" and we write it as follows: 2) The symbol √ is used to denote the square root of a number. 3) A Square root of the whole number by factorization: To find the square root of a number which is a perfect square, express the number as the product of prime factors. Now, take the product of these prime factors choosing one out of every pair of the same primes. 4) Square root by division: To find the square root by division: Step 1: Group the digits of the number in the pairs of two digits starting from the right-hand side. For example, if the number is 330625, there would be three pairs of digits which include 33, 06, and 25. Each pair of digits and the remaining digit if any is called a period, so there are three periods. Step 2: Find a number whose square is either equal to or less than the first pair or period on the left of the number. For example: the square of a number ≤ 33. In this case, 5*5 = 25 ≤ 33. Use this number (5) as a divisor and also as the quotient. 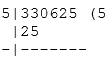
Step 3: Subtract the product of the divisor and the quotient from the first pair and put the next pair to the right of the remainder. This number becomes the new dividend. 
Step 4: Create new divisor by taking two times the quotient and annexing it with a suitable digit which is also taken as the next digit of the quotient. The product of this new divisor and the digit should be equal to or less than the new dividend. 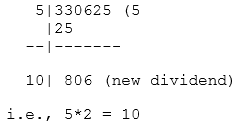
Now annexing a new digit 7 with 10, because if we annexing a digit less than 7, the product of the new divisor (it can be either 101, 102, 103,... 106) and the annexing digit will not reach up to the nearby value. Therefore 107 is treated as a new divisor, and it will give a nearby value to the new dividend. Step 5: Repeat the 2, 3 and 4th step till all the pairs or periods are taken up. The quotient so obtained is the required square root of the given number. 
5) How to find the square root of numbers in the decimal form: Step 1: Make the number of decimal places even by placing a zero on the right of the decimal part, if required. For example, 41.2 = 41.20 (0 is added to make the decimal places even). Step 2: In the integral part make the pairs or periods like we made in the above example. i.e., 41 is a pair Step 3: In the decimal part, mark the periods on every pairs of digits starting with the first decimal place. i.e., 20 is a pair Step 4: Now, find the square root by long division method. Step 5: Place the decimal point in the square root as soon as the integral part is exhausted. For example: 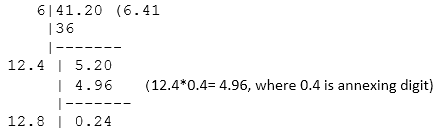
Now we can add the pair of zero after decimal place (there will no change in the number) 
(Here we assume that the square root of the decimal number (41.2) is 6.41 (upto two decimal places)). 6) Cube Root: The cube root of a given number x is the number whose cube is x. We denote the cube root of a by 7) Determination of Cube Root: Resolve the given number as the product of prime factors and take the product of prime factors, choosing one out of three of the same prime factors. Aptitude Square Roots and Cube Roots Test Paper 1 Aptitude Square Roots and Cube Roots Test Paper 2 Aptitude Square Roots and Cube Roots Test Paper 3 Aptitude Square Roots and Cube Roots Test Paper 4 |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





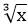 .
.




