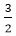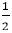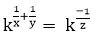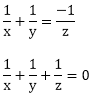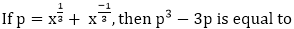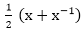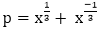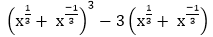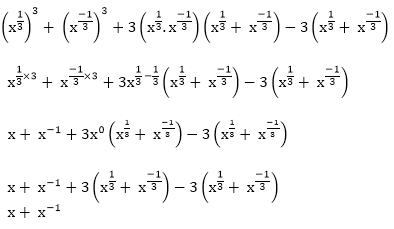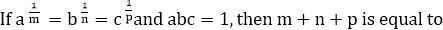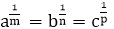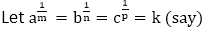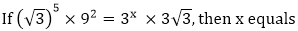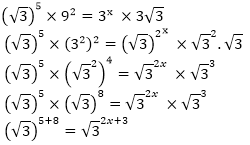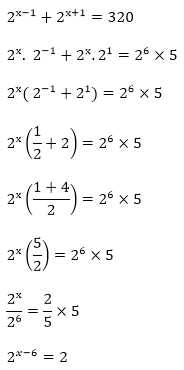Surds and Indices Aptitude Test Paper 311) If 2x=3y=6-z, then
Answer: A Explanation: Given: 2x=3y=6-z Equating the powers of above equation because the base is same 12)
Answer: C Explanation: Given: Then p3-3p Putting the value of 'p' in above equation
By applying (a+b)3 = a3 + b3 + 3ab(a+b)
13)
Answer: C Explanation: Given:
Then, a = km, b = kn, c = kp abc = 1 (given) km. kn. kp = k0 km+n+P = k0 m+n+P = 1 Since the base are same So, m+n+P = 0 14)
Answer: D Explanation:
By equating the power 5 + 8 = 2x +3 15) If 2x-1+2x+1=320,then x is equal to
Answer: D Explanation:
By equating the powers x-6 = 1 Surds and Indices Test Paper 1 Surds and Indices Test Paper 2 Surds and Indices Test Paper 4 Surds and Indices Concepts
Next TopicSurds and Indices Aptitude Test Paper 4
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





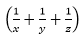 is equal to
is equal to