Area of a Triangle
In this section, we will learn triangle definition, types of triangles, area of triangle formula, derivation, and how to find the area of a trainable along with examples in detail.
Triangle
A triangle is a polygon having three vertices and three edges. The sum of three interior angles is 180 degrees. The following diagram represents a triangle.
Types of triangle
There are three types of triangles:
- Equilateral Triangle
- Isosceles Triangle
- Scalene Triangle
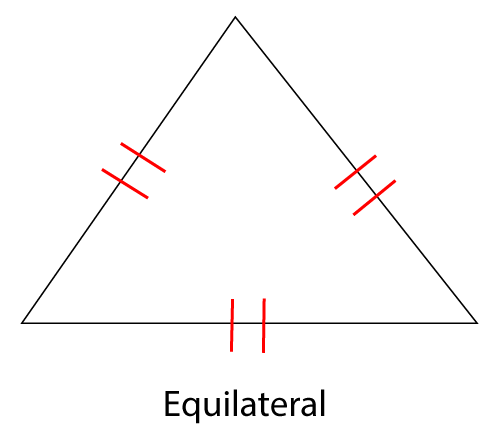
Equilateral Triangle
An equilateral triangle has three sides of equal length and three equal angles. Each angle is of 60 degrees. It has three lines of symmetry.
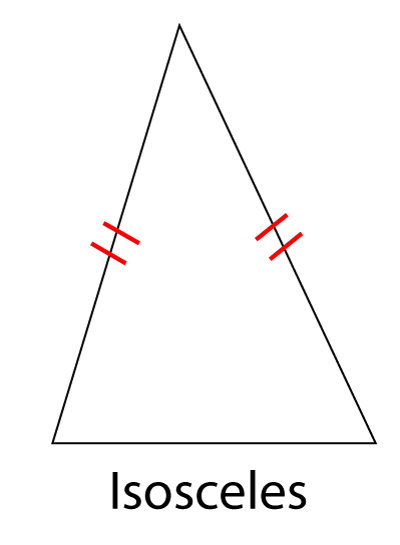
Isosceles Triangle
An isosceles triangle has two sides of equal length and two equal angles. It has one line of symmetry.
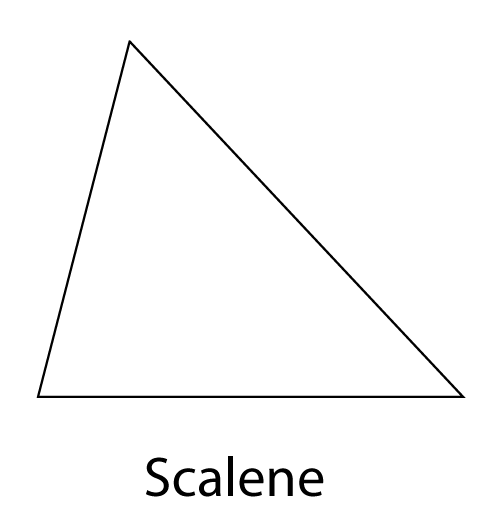
Scalene Triangle
A scalene triangle has no sides of equal length and no equal angles. It has no line of symmetry.
Area of a Triangle
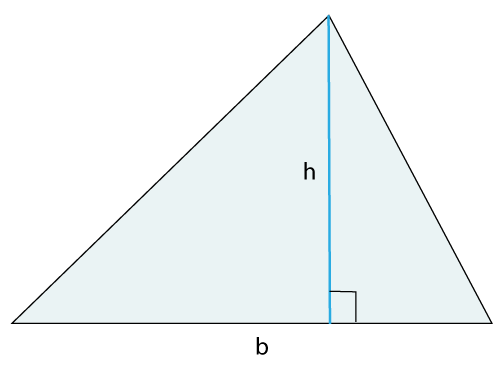
The area of a triangle is the region covered by a triangle. The area of a triangle is equal to half of the base multiplied by the perpendicular height of the triangle.
If the given triangle is a right triangle, multiply the two sides together, which are adjacent to the right angle.
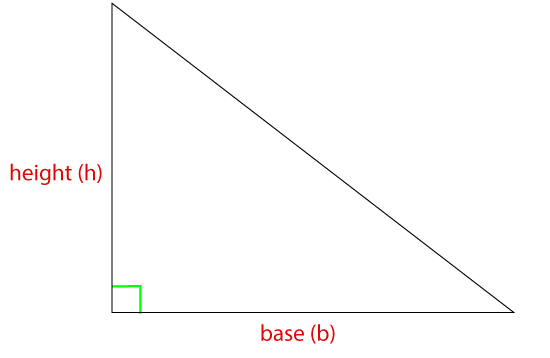
If the given triangle is not a right triangle, first find the perpendicular height of the triangle by dropping a vertical line down from the highest point on the triangle to the base, as we have shown in the following figure.
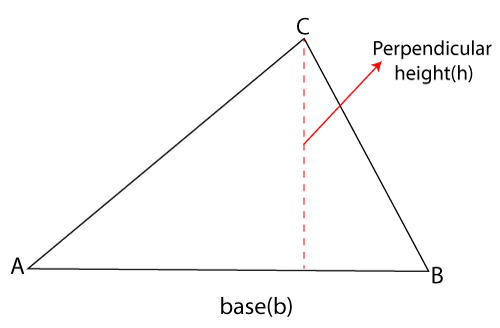
Area of Triangle Formula
Two formulas are used to find the area of a triangle.
It is the half of the base multiplied by the height. The formula given below works for all triangles.
Where b denoted the base and h denote the height of the given triangle.
Note: We can choose any side of the triangle as a base but make sure that height is measured at right angles to the base.
Heron's Formula
Heron's formula applied when all three sides of a triangle are given, or the three sides are unequal.
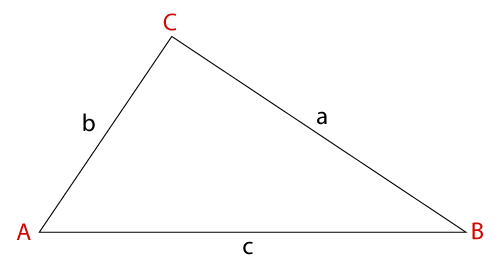
It includes two important steps:
Step 1: First, calculate the semi-perimeter (s) by adding the length of three sides of the triangle and divide the sum by 2.
semi-perimeter (s) = (a + b + c) / 2
Where a, b, c is the length of the sides.
Step 2: Apply the semi-perimeter and three sides a, b, c of the triangle in the formula to find the area of a triangle.
Area of a Triangle (A) = √(s (s-a)(s-b)(s-c) )
We can also find the area of a triangle when two sides and an angle is known. But the Heron's formula does not work for the same. The formula depends on which sides and angles are given. Let's see the formulas for different sides and angles.
- When the sides a, b and the angle C is given then the formula for area of a triangle will be:
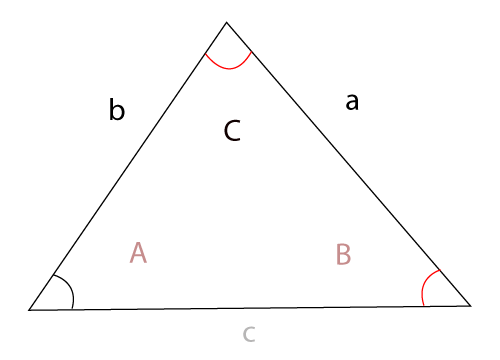
Area of a Triangle (A) = ½ ab sin C
- When the sides b, c, and the angle A is given then the formula for the area of a triangle will be:
Area of a Triangle (A) = ½ bc sin A
- Similarly, when the sides c, a, and the angle B is given, then the formula for the area of a triangle will be:
Area of a Triangle (A) = ½ ca sin B
Area of an Equilateral Triangle
An equilateral triangle has three sides of equal length.
Area of an equilateral triangle (A) =  a2 a2
Where a is the length of a triangle.
Area of an Isosceles Triangle
Area of an Isosceles triangle (A) = ½ (base × height)
Derivation
Let's see why the area of a triangle is half of b*h.
- Draw a triangle whose base is b and height is h, as shown below.
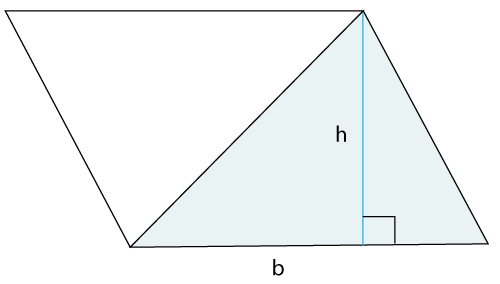
- In the newly created triangle, draw a perpendicular.
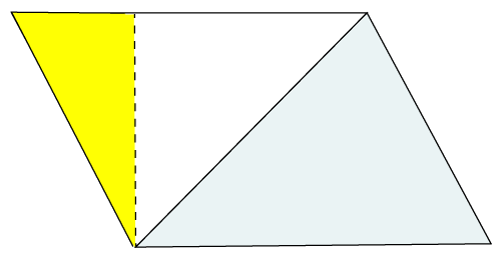
- Cut a triangle (yellow part) and move it to the right, as we have in the following image.
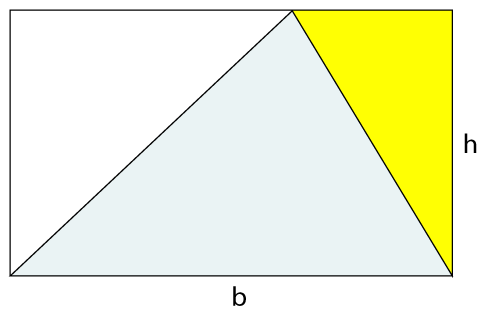
We see that the triangle is now converted into a rectangle. We know the formula of area of a rectangle:
Area of rectangle (A) = length * width
i.e. is (b*h).
The base multiplied by height is twice the area of the triangle (represented in blue color). But we have to find the area of a triangle i.e.
Therefore, the area of a triangle is half of the base*height.
Therefore, the area of a triangle is half of the base*height.
How to Find Area of a triangle
When base and height is given
Example 1: Find the area of a triangle whose height is 20 cm and the base is 15 cm.
Solution:
Given, base (b) = 15 cm, height (h) = 20 cm
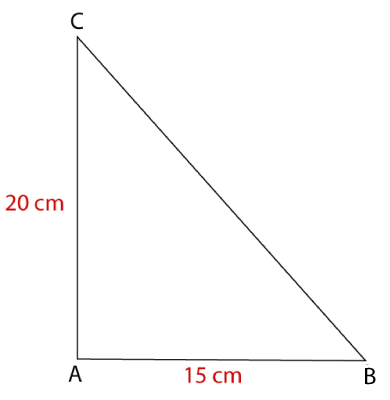
We know that,
Area of Triangle (A) = ½ bh
Putting the values, we get:
A = ½ 15 * 20
A = 150 sq. cm.
The area of the triangle is 150 sq. cm.
Example 2: Find the area of the triangle given below.
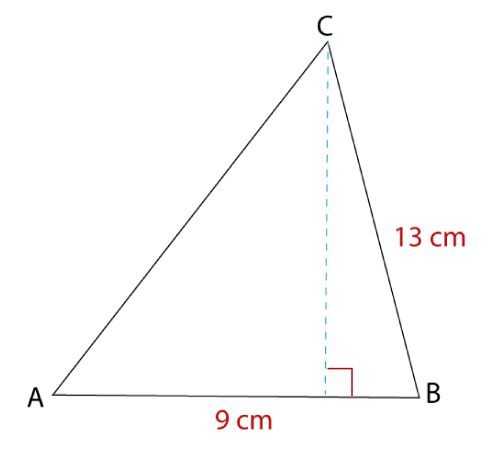
Solution:
Given, base (b) = 9 m, height (h) = 13 m
We know that,
Area of Triangle (A) = ½ bh
Putting the values, we get:
A = ½ 9 * 13
A = 58.5 m2
The area of triangle is 58.5 m2.
Example 3: The base of an obtuse triangle is 6.6 inches, and the height is 14.7 inches. Find the area of the triangle.
Solution:
Given, base (b) = 6.6 inches, height (h) = 14.7 inches
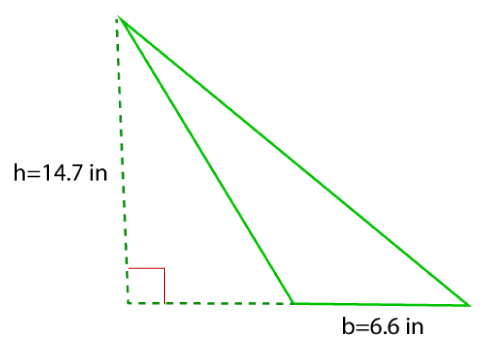
We know that,
Area of Triangle (A) = ½ bh
Putting the values, we get:
A = ½ 6.6 * 14.7
A = 48.51 inches2
The area of the triangle is 48.51 inches2.
Example 4: Find the area of the triangle given below.
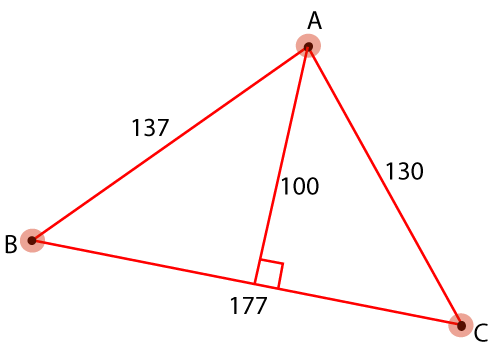
Solution:
From the above figure, base (b) = 177 cm.
Note: We will consider the height that makes the right angle on the base that is 100 cm. We will not consider 130 as height because it doesn't make the right angle.
We know that,
Area of Triangle (A) = ½ bh
Putting the values, we get:
A = ½ 177 * 100
A = 8850 sq. cm
The area of the triangle is 8850 sq. cm.
When the length of three sides is given
Example 5: Find the area of a triangle whose all sides are 7 cm long.
Solution:
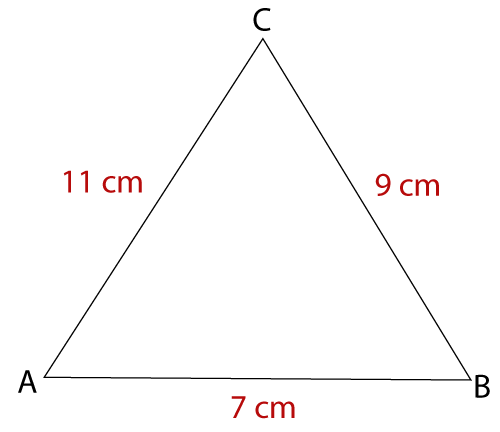
Given, a = 7 cm, b = 9 cm, c = 11 cm
In this question, the length of all three sides is given. So, we will apply Heron's formula.
Area of a Triangle (A) = √(s (s-a)(s-b)(s-c) )
First, we will calculate semi-perimeter (s).
s = (7 + 9 + 11) / 2
s = 13.5 cm
Putting the values in the above formula, we get:
A = √(13.5 (13.5-7)(13.5-9)(13.5-11) )
A = √(13.5 (6.5)(4.5)(2.5) )
A = √987.1875
A = 31.41 sq. cm.
The area of the triangle is 31.41 sq. cm.
When SAS (side-angle-side) is given
Example 6: Find the area of a triangular land whose side AB is 125 m and side BC is 220 m. The angle between AB and BC is .
Solution:
First, draw a triangle according to the given information:
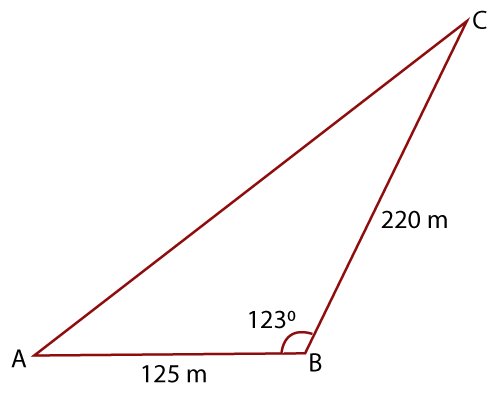
Given, BC = a= 220 m, AB = c = 125 m, and angle B = 123°
We know that,
Area of triangle (A) = ½ ac sin B
A = ½ (220 * 125) * (sin )
A = ½ (27500) * (0.83867)
A = ½ (23063.4407)
A = 11,532 m2
The area of triangle is 11,532 m2.
Example 7: Find the area of the triangle given below.
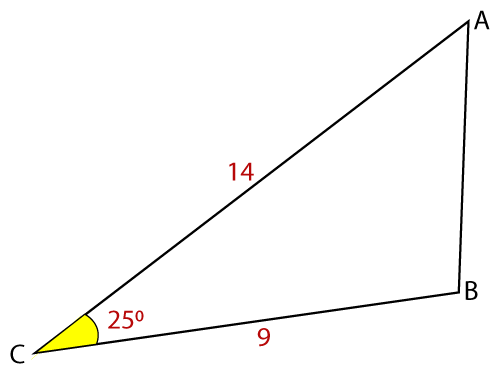
Solution:
Given, CB = a = 9 cm, AC = b = 14 cm, and angle C is 25°
We know that,
Area of triangle (A) = ½ ab sin C
A = ½ (9 * 14) * (sin 25°)
A = ½ (126) * (0.42261)
A = ½ (53.24886)
A = 27 cm2
The area of triangle is 27 cm2.
Area of an equilateral triangle
Example 8: In an equilateral triangle, a side is ten cm long, find the area of the triangle.
Solution:
Given, a = 10 cm
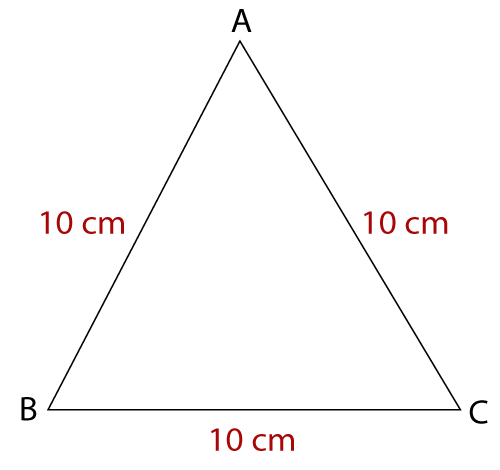
We know the formula of area of an equilateral triangle:

| 





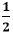 bh
bh
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now










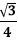 a2
a2


















