Area of Rectangle

A rectangle is a polygon that has four sides. The property of a rectangle is that the length of the opposite sides must be equal. We can find the area of a rectangle by using the formula that includes height and width.

In this section, we will learn how to find the area of a rectangle and will try to understand through examples given in the last of this section.

Definition

The area of a rectangle is the reign covered by a rectangle in a 2D plane. In other words, the width multiplied by its height. The unit of area is square units.

Area of Rectangle Formula

We can calculate the area of a rectangle if we know its height and length.

Where w represents the width, and h represents the height.

Sometimes we have given diagonal and width of a rectangle. Then we apply the following formula to find the area of a rectangle.

Properties of Rectangle

• All sides of a rectangle are parallel and equal to each other.
• Each right angle is 90° degrees.
• All sides have equal length.
• A square is always a rectangle.

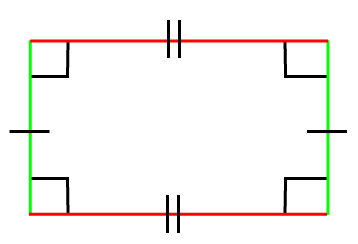
In the above figure, the red color sides are of the same length and parallel to each other. Similarly, the green color sides are of the same length and parallel to each other. The right angle inside the rectangle denotes the angle, each of 90°.

Example

When width and height are given

Example 1: Find the area of a rectangle whose height is 5 m and width is 9 m.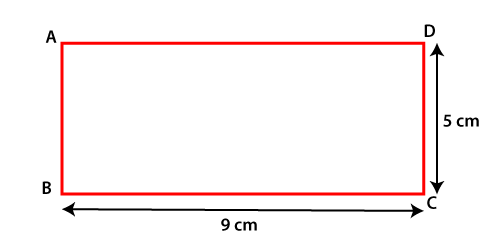

Solution:

Given, h=5 m and w=9 m

We know that,

area of rectangle (A) = w * h

putting the values in the above formula, we get

The area of the rectangle is 45 m².

When diagonal and width is given

Example 2: Find the area of a rectangular board whose diagonal length is 20 cm and width is 13 cm.

Solution:

Given, length of diagonal (d) = 20 and width is 13 cm

We know that,

Area of rectangle (A) = width√diagonal²-width²

A = 13 √20²-13²2

A = 13 √(400-169)

A = 13 √231

A = 13 * 15.19

A = 197.58 cm²

The area of rectangle is 197.58 cm².

Using Pythagoras theorem

Example 3: If the diagonal of a rectangle ABCD is 100 cm and its length x is twice its width y. Find the area of the rectangle.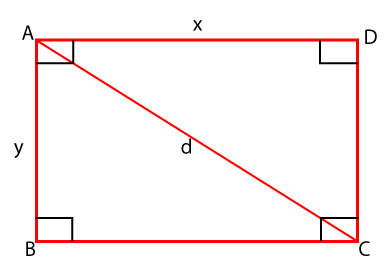

Solution:

Given, diagonal (d) = 100 cm and width (x)= 2y

According to the Pythagoras theorem:

Hypotenuse=√base²+perpendicular²

Putting the values in the above equation, we get:

100²= y² + (2y)²

100²= y² + 4y²

100²= 5y²

on solving the above equation,

y=20√5

putting the value of y in width, we get:
x = 40√5 cm.

we know that,

Area of triangle (A) = width * height

Since,

A = 40√5 cm²

The area of rectangle is 40√5 cm².