Area of Rectangular Prism

A rectangular prism refers to a 3-Dimensional object with six sides that are rectangles. The six sides come in 3 pairs of parallel sides. For example, Brick. In this article, we will learn how to find the surface area of the rectangular prism.

Determining the surface area

The given figure depicts the diagram of a rectangular prism with length l, width w, and height h located next to the three different edges of the shape. If you are unable to decide the side, represent the three-line that meets at that corner.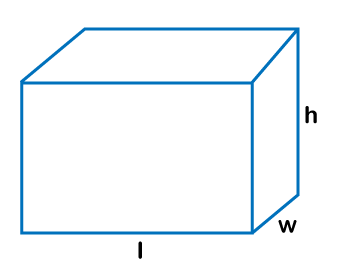

Let's understand this concept with the help of an example.

Consider an empty box that has a base has base that measures 5 inches by 6 inches, and it stands 8 inches tall. The large size of the base is 6 inches, so the length = 6, w = 5, and h = 8

Considering the six faces of the prism

To cover the whole surface area, you need to consider six different "faces."

In a rectangular prism, both the top and bottom faces are the same in size.
In a rectangular prism, both the front and back faces are the same in size.
In a rectangular prism, both the left and right faces are the same in size.

Calculate the area of the bottom face:

finding the surface area of just one face (in our case, bottom). It forms a rectangle shape, just the same as each face. One edge of the rectangle is considered as length, and another one is considered as width. If you want to calculate the rectangle area, you need to multiply the two edges together. Area of the bottom edge = length * Width.

Consider an example we have mentioned above, the length of the prism is considered as 6 inches and width is 5 inches, so the area of the bottom face is 6 inches x 5 inches = 30 square inches.

Finding the area of the top face:

Previously we have already discussed that the top and bottom faces are the same in size. It must have an area of length * Width.

We have already calculated; the top area is 30 square inches.

Finding the area of the front and back faces:

Go through the previous diagram and see the front face: the one with one edge shown width and another one is shown height. So, the area of the front face = Width * Height, and the back area is the same Width * Height.

In the above example, w = 5 inches and h = 8 inches, so the front area is 5 inches x 8 inches = 40 square inches.

Finding the area of the left and right faces:

In the above example, we have already calculated the two faces, each the same size. We have considered the one edge as the length of the prism, and the one edge is the height of the prism. Here, the area of the left face is length × height, and the area of the right face is length × height.

In the above example, we have found the l = 6 and h = 8 inches, so the area of the left face = 6 inches x 8 inches = 48 square inches.

Now, you need to sum all the six areas together; you've found the area of each of the six faces. Sum up all the values together to get the area of the whole shape: lw + lw + wh + wh + LH + lh. To find the area of any rectangular Prism, you can use this formula,

Here, we need to just sum up the determined value of the six areas of six faces of the rectangular prism: 30 + 30 + 40 + 40 + 48 + 48 = 94 square inches.

Method 2

Deriving the formula in the simple form

Simplify the formula to calculate the area of a rectangular prism

Now you know the concept to find the surface area of any rectangular prism. You can do it easily if you have learned the basic concept of algebra. We have already studied the area of a rectangular prism = lw + lw + wh + wh + LH + lh. If we add all the term that is the same, we get:

Area of a rectangular prism = 2lw + 2wh + 2lh

= 2 (lw + wh + LH)