Assumptions of Cronbach's Alpha in SPSS

In this section, we are going to learn about the assumptions of Cronbach's alpha in SPSS. Now we have seen people indiscriminately apply the Cronbach alpha without even bothering for the assumptions. That's fine if we have a large sample size. We can take little liberty with the assumptions. It is often good to be aware of the assumptions of any test that we are using. So in the case of Cronbach's alpha, there are two fundamental assumptions or two main assumptions.

First assumption of Cronbach's Alpha

• The first assumption is that there is no correlation between the error terms. In the previous section, we saw that we discuss a typical measure model of a reflective scale that is again presented here.

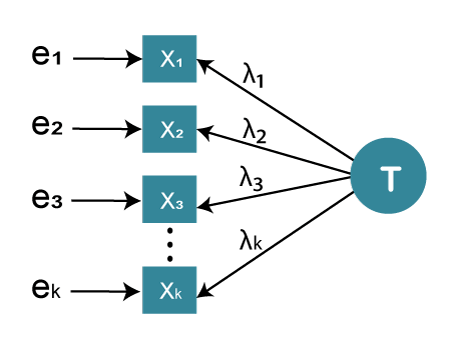
• In the case of a reflective scale, there is the main construct that is denoted by symbol T. And then we have the indicators of the scale that is the items of the scale that we have written or constructed. They are represented by X₁, X₂, till X_k. In the case of a reflective scale, these items are a reflection of its main construct. If the main construct is happiness, we can take X₁ like smiling more often or being very satisfied in their life, because a high level of positive emotion and high level of satisfaction are basic aspects or reflection of happiness.
• If somebody is happier, we can imagine that the person is to be more smiling and more satisfied with life. So there could be many indicators like X₁, X₂, but these indicators cannot capture happiness in the fullest extent. Every time they are bound to be an extra amount of error.
• For example, suppose we measure happiness while smiling. So X₁ is smiling, and T is happiness, λ is the factor loading. There must be some unexplained variance in that case, and that is going to be denoted by symbol e1, and that is the error.
• One thing we can fairly imagine that we have a main construct, and the main construct is being measured through different indicators, and these indicators are a reflection of the main construct. That's why arrows are flowing from the main construction to the indicator. Basically, it's a kind of regression model in which indicators are being predicted by the construct and not the visa versa. If there is a visa versa situation where indicators are predicting constructs, that is the formative scale. In the case of a reflective scale, it is the construct that predicts the indicator, and this indicator is capturing an amount of variance in the happiness or the main construct.
• Now for variance, there is a fight between two persons. One is our indicator, another the error term related to the indicator. So happiness is the main construct, and an indicator wants to predict happiness, and there is an error term as well. In the null situation, 50% of the variation in the happiness score may be reflected by the indicator and 50% through the error term related to the indicator 1.
• An indicator will be a good indicator only when it explains more amount of variation in happiness than the error term. So the 50-50 situation is not desirable. We are basically hypothesizing that they are jostling for the explaining variance in happiness. But indicator should explain more variance in the construct as compared to the error term.
• If indicators are winning the war, in that case, we can say they are truly reflecting the main construct. They measure the main construct If error terms are winning the war, we can say we have created poor indicators, and our indicators cannot explain a good amount of variance. Suppose indicators explain 40% of the variance, and the error term explains around 60% variance, which is not a desirable situation. Indicators should explain more amount of variance.
• The measure assumption before calculating Cronbach's alpha is that these error terms should not be correlated. Indicators can be correlated, but their respective error term should not be correlated. If error terms are correlated in that case, our indicators are useless or meaningless. Whenever we create a scale model or do a reliability analysis, always be careful about the error We have to make sure that error terms are not correlated to each other. If they correlate, the assumptions of Cronbach's alpha have been violated.

Second Assumptions of Cronbach's alpha

• The Second important assumption of Cronbach's alpha is that the items are tau-equivalent. Tau-equivalent is a kind of model. We don't need to worry about the model. We already have a model. In the model, we have main construct T, which is predicting the indicators X₁, X₂, X₃ and this λ₁, λ₂, λ₃ are factor loadings. When we convert it into standardized loading, they become the standardized regression coefficient. So we already have a model, and it's a kind of regression model.

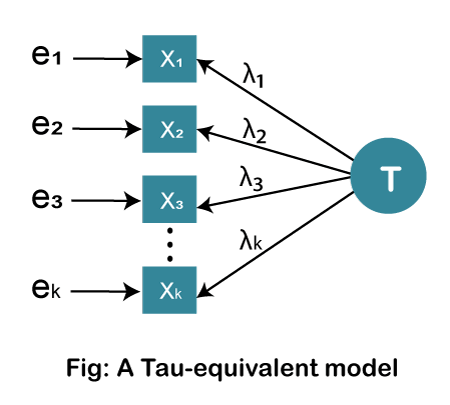
• A tau-equivalent model is a kind of model in which all the factor loadings are the same.

• A tau-equivalent model is a special type of Congeneric model where all factor loading of different indicators is assumed to be the same. The congeneric model is a model in which all factor loading freely In contrast to this, the tau-equivalent model is a model in which all the factor loadings are equivalent to each other.
• When we are creating Cronbach or doing to the reliability analysis, we are assuming that all these indicators are equally important. It's not that one indicator is very important as compared to other indicators. It might be the situation when one indicator is more important than other indicators. In fact, this is the more realistic situation in which indicators are differentially important. But the fundamental assumption is that all the indicators are almost equally important, and that is dependent on their factor loading.