AVL Tree Program in C

What Is an AVL Tree?

Adelson-Velskii and Landis are the people who discovered it, so the name came from their names i.e., AVL. It is commonly referred to as a height binary tree. An AVL tree is one that has one of the following characteristics at each of its nodes.

If a node's longest path in its left subtree is longer than its longest path in its right subtree, the node is said to be "left heavy."

If the longest path in a node's right subtree is one more long than the longest path in its left subtree, the node is said to be "right heavy."

If the longest paths in the right and left subtrees are equal, a node is said to be balanced.

The AVL tree is a height-balanced tree where each node's right and left subtree height differences are either -1, 0 or 1. A factor known as the balance factor keeps the subtrees' height differences apart. As a result, we can define AVL as a balanced binary search tree in which each node's balance factor is either -1, 0 or +1. In this case, the formula follows to determine the balancing factor:

Balance factor properties -

If a subtree has a balance factor greater than zero, it is said to be left-heavy because the height of the left subtree is greater than the height of the right subtree, implying that the left subtree contains more nodes than the right subtree.
If a subtree has a balance factor of 0, it is said to be right-heavy because the height of the left subtree is less than the height of the right subtree, implying that the right subtree has more nodes than the left subtree.
If the balance factor is zero, the subtree is perfectly balanced, with equal heights in both the left and right subtrees.

The AVL Tree's rotations:

If any node of the tree falls out of balance, the necessary rotations are carried out to correct the imbalance.

AVL Tree Operations in C

In the AVL tree, there are three types of operations that are performed:

A New Node is Inserted
Removal of a Node
removing a node from the right subtree
removing of a Node from the Left Subtree
Looking for a Node in an AVL Tree

To carry out these operations, we must perform the four types of rotations. Four different rotational kinds are possible and are used under various scenarios as follows:

LL Rotation: When a new node is added as the left child of the unbalanced node's left subtree.

RR Rotation: When a new node is added as the right child of the right subtree of an unbalanced node, this process is known as RR Rotation.

LR Rotation: When a new node is added as the left child of an unbalanced node's right subtree.

RL Rotation: When a new node is added as the right child of an unbalanced node's left subtree.

Implementation:

Insertion in AVL Tree: To ensure that the given tree remains AVL after each insertion, we must add some re-balancing to the standard BST insert operation.

The two basic operations that can be used to balance a BST without violating the BST property are as follows (keys(left) < key(root) < keys(right)).

Left Rotation
Right Rotation

Insertion procedures include the following steps:

Allow the newly added node to be w
Insert the standard BST insert for w.
Travel up from w to find the first unbalanced node. Allow z to be the first unbalanced node, y to be z's child on the path from w to z, and x to be z's grandchild on the path from w to z.
Rebalance the tree by performing the necessary rotations on the z-rooted subtree. As x, y, and z can be arranged in four different ways, there are four possible cases that must be handled.
The four possible arrangements are as follows:
y is z's left child, and x is y's left child (Left Left Case)
y is z's left child, and x is y's right child (Left Right Case)
y is z's right child, and x is y's right child (Right Right Case)
sy is z's right child, and x is y's left child (Right Left Case).

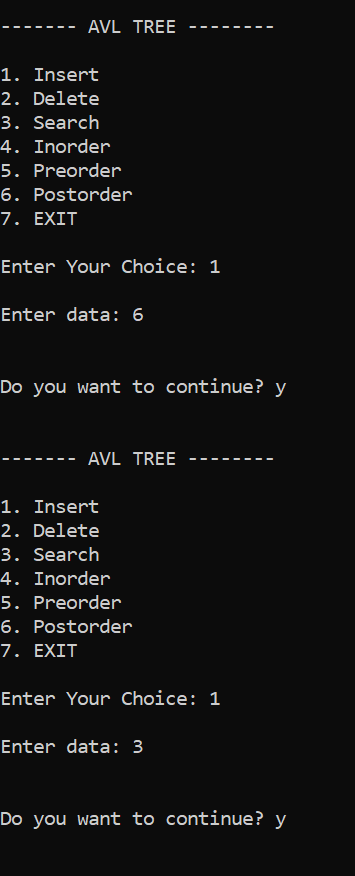
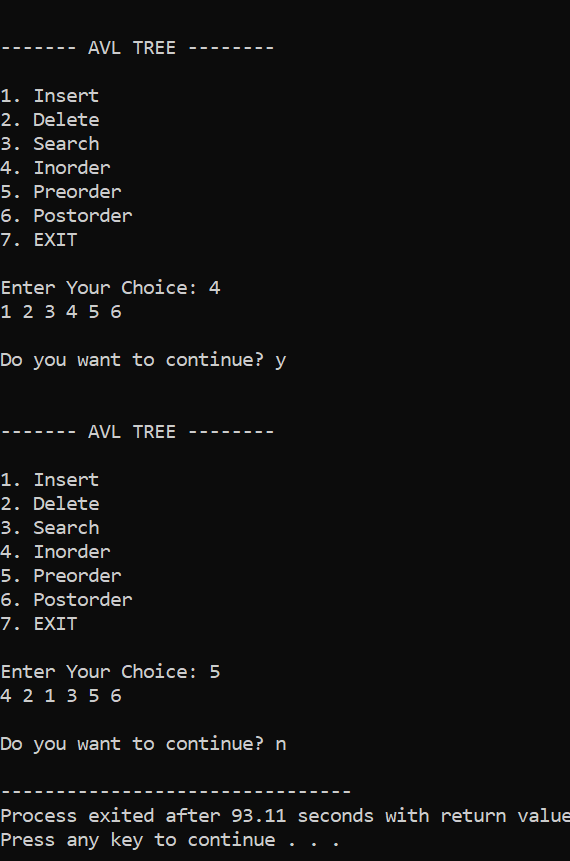
AVL Tree Program in C

Program 1:

#include <stdio.h>
#include <stdlib.h>
 
struct Node
{
    int key;
    struct Node *left;
    struct Node *right;
    int height;
};
 
int getHeight(struct Node *n){
    if(n==NULL)
        return 0;
    return n->height;
}
 
struct Node *createNode(int key){
    struct Node* node = (struct Node *) malloc(sizeof(struct Node));
    node->key = key;
    node->left = NULL;
    node->right = NULL;
    node->height = 1;
    return node;
}
 
int max (int a, int b){
    return (a>b)?a:b;
}
 
int getBalanceFactor(struct Node * n){
    if(n==NULL){
        return 0;
    }
    return getHeight(n->left) - getHeight(n->right);
}
 
struct Node* rightRotate(struct Node* y){
    struct Node* x = y->left;
    struct Node* T2 = x->right;
 
    x->right = y;
    y->left = T2;
 
    x->height = max(getHeight(x->right), getHeight(x->left)) + 1;
    y->height = max(getHeight(y->right), getHeight(y->left)) + 1;
 
    return x;
}
 
struct Node* leftRotate(struct Node* x){
    struct Node* y = x->right;
    struct Node* T2 = y->left;
 
    y->left = x;
    x->right = T2;
 
    x->height = max(getHeight(x->right), getHeight(x->left)) + 1;
    y->height = max(getHeight(y->right), getHeight(y->left)) + 1;
 
    return y;
}
 
struct Node *insert(struct Node* node, int key){
    if (node == NULL)
        return  createNode(key);
 
    if (key < node->key)
        node->left  = insert(node->left, key);
    else if (key > node->key)
        node->right = insert(node->right, key);
 
    node->height = 1 + max(getHeight(node->left), getHeight(node->right));
    int bf = getBalanceFactor(node);
 
    // Left Left Case
        if(bf>1 && key < node->left->key){
            return rightRotate(node);
        }
    // Right Right Case
        if(bf<-1 && key > node->right->key){
            return leftRotate(node);
        }
    // Left Right Case
    if(bf>1 && key > node->left->key){
            node->left = leftRotate(node->left);
            return rightRotate(node);
        }
    // Right Left Case
    if(bf<-1 && key < node->right->key){
            node->right = rightRotate(node->right);
            return leftRotate(node);
        }
    return node;
}
 
void preOrder(struct Node *root)
{
    if(root != NULL)
    {
        printf("%d ", root->key);
        preOrder(root->left);
        preOrder(root->right);
    }
}
 
int main(){
    struct Node * root = NULL;
 
 
    root = insert(root, 1);
    root = insert(root, 2);
    root = insert(root, 4);
    root = insert(root, 5);
    root = insert(root, 6);
    root = insert(root, 3);
    preOrder(root);
    return 0;
}

Output

4 2 1 3 5 6

Representation: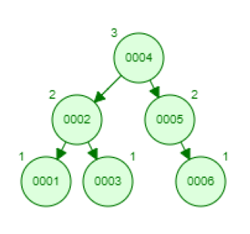

As a result, we got the above AVL tree after inserting those elements. The preorder traversal of the above AVL tree is 4->2->1->3->5->6.

Program 2:

/*
 * AVL Tree Program in C
 */
 
#include<stdio.h>
#include<stdlib.h>
 
// structure of the tree node
struct node
{
    int data;
    struct node* left;
    struct node* right;
    int ht;
};
 
// global initialization of root node
struct node* root = NULL;
 
// function prototyping
struct node* create(int);
struct node* insert(struct node*, int);
struct node* delete(struct node*, int);
struct node* search(struct node*, int);
struct node* rotate_left(struct node*);
struct node* rotate_right(struct node*);
int balance_factor(struct node*);
int height(struct node*);
void inorder(struct node*);
void preorder(struct node*);
void postorder(struct node*);
 
int main()
{
    int user_choice, data;
    char user_continue = 'y';
    struct node* result = NULL;
 
    while (user_continue == 'y' || user_continue == 'Y')
    {
        printf("\n\n------- AVL TREE --------\n");
        printf("\n1. Insert");
        printf("\n2. Delete");
        printf("\n3. Search");
        printf("\n4. Inorder");
        printf("\n5. Preorder");
        printf("\n6. Postorder");
        printf("\n7. EXIT");
 
        printf("\n\nEnter Your Choice: ");
        scanf("%d", &user_choice);
 
        switch(user_choice)
        {
            case 1:
                printf("\nEnter data: ");
                scanf("%d", &data);
                root = insert(root, data);
                break;
 
            case 2:
                printf("\nEnter data: ");
                scanf("%d", &data);
                root = delete(root, data);
                break;
 
            case 3:
                printf("\nEnter data: ");
                scanf("%d", &data);
                result = search(root, data);
                if (result == NULL)
                {
                    printf("\nNode not found!");
                }
                else
                {
                    printf("\n Node found");
                }
                break;
            case 4:
                inorder(root);
                break;
 
            case 5:
                preorder(root);
                break;
 
            case 6:
                postorder(root);
                break;
 
            case 7:
                printf("\n\tProgram Terminated\n");
                return 1;
 
            default:
                printf("\n\tInvalid Choice\n");
        }
 
        printf("\n\nDo you want to continue? ");
        scanf(" %c", &user_continue);
    }
 
    return 0;
}
 
// creates a new tree node
struct node* create(int data)
{
    struct node* new_node = (struct node*) malloc (sizeof(struct node));
 
    // if a memory error has occurred
    if (new_node == NULL)
    {
        printf("\nMemory can't be allocated\n");
        return NULL;
    }
    new_node->data = data;
    new_node->left = NULL;
    new_node->right = NULL;
    return new_node;
}
 
// rotates to the left
struct node* rotate_left(struct node* root)
{
    struct node* right_child = root->right;
    root->right = right_child->left;
    right_child->left = root;
 
    // update the heights of the nodes
    root->ht = height(root);
    right_child->ht = height(right_child);
 
    // return the new node after rotation
    return right_child;
}
 
// rotates to the right
struct node* rotate_right(struct node* root)
{
    struct node* left_child = root->left;
    root->left = left_child->right;
    left_child->right = root;
 
    // update the heights of the nodes
    root->ht = height(root);
    left_child->ht = height(left_child);
 
    // return the new node after rotation
    return left_child;
}
 
// calculates the balance factor of a node
int balance_factor(struct node* root)
{
    int lh, rh;
    if (root == NULL)
        return 0;
    if (root->left == NULL)
        lh = 0;
    else
        lh = 1 + root->left->ht;
    if (root->right == NULL)
        rh = 0;
    else
        rh = 1 + root->right->ht;
    return lh - rh;
}
 
// calculate the height of the node
int height(struct node* root)
{
    int lh, rh;
    if (root == NULL)
    {
        return 0;
    }
    if (root->left == NULL)
        lh = 0;
    else
        lh = 1 + root->left->ht;
    if (root->right == NULL)
        rh = 0;
    else
        rh = 1 + root->right->ht;
 
    if (lh > rh)
        return (lh);
    return (rh);
}
 
// inserts a new node in the AVL tree
struct node* insert(struct node* root, int data)
{
    if (root == NULL)
    {
        struct node* new_node = create(data);
        if (new_node == NULL)
        {
            return NULL;
        }
        root = new_node;
    }
    else if (data > root->data)
    {
        // insert the new node to the right
        root->right = insert(root->right, data);
 
        // tree is unbalanced, then rotate it
        if (balance_factor(root) == -2)
        {
            if (data > root->right->data)
            {
                root = rotate_left(root);
            }
            else
            {
                root->right = rotate_right(root->right);
                root = rotate_left(root);
            }
        }
    }
    else
    {
        // insert the new node to the left
        root->left = insert(root->left, data);
 
        // tree is unbalanced, then rotate it
        if (balance_factor(root) == 2)
        {
            if (data < root->left->data)
            {
                root = rotate_right(root);
            }
            else
            {
                root->left = rotate_left(root->left);
                root = rotate_right(root);
            }
        }
    }
    // update the heights of the nodes
    root->ht = height(root);
    return root;
}
 
// deletes a node from the AVL tree
struct node * delete(struct node *root, int x)
{
    struct node * temp = NULL;
 
    if (root == NULL)
    {
        return NULL;
    } 
 
    if (x > root->data)
    {
        root->right = delete(root->right, x);
        if (balance_factor(root) == 2)
        {
            if (balance_factor(root->left) >= 0)
            {
                root = rotate_right(root);
            }
            else
            {
                root->left = rotate_left(root->left);
                root = rotate_right(root);
            }
        }
    }
    else if (x < root->data)
    {
        root->left = delete(root->left, x);
        if (balance_factor(root) == -2)
        {
            if (balance_factor(root->right) <= 0)
            {
                root = rotate_left(root);
            }
            else
            {
                root->right = rotate_right(root->right);
                root = rotate_left(root);
            }
        }
    }
    else
    {
        if (root->right != NULL)
        { 
            temp = root->right;
            while (temp->left != NULL)
                temp = temp->left;
 
            root->data = temp->data;
            root->right = delete(root->right, temp->data);
            if (balance_factor(root) == 2)
            {
                if (balance_factor(root->left) >= 0)
                {
                    root = rotate_right(root);
                }
                else
                {
                    root->left = rotate_left(root->left);
                    root = rotate_right(root);
                }
            }
        }
        else
        {
            return (root->left);
        }
    }
    root->ht = height(root);
    return (root);
}
 
// search a node in the AVL tree
struct node* search(struct node* root, int key)
{
    if (root == NULL)
    {
        return NULL;
    }
 
    if(root->data == key)
    {
        return root;
    }
 
    if(key > root->data)
    {
        search(root->right, key);
    }
    else
    {
        search(root->left, key);
    } 
}
 
// inorder traversal of the tree
void inorder(struct node* root)
{
    if (root == NULL)
    {
        return;
    }
 
    inorder(root->left);
    printf("%d ", root->data);
    inorder(root->right);
}
 
// preorder traversal of the tree
void preorder(struct node* root)
{
    if (root == NULL)
    {
        return;
    }
 
    printf("%d ", root->data);
    preorder(root->left);
    preorder(root->right);
}
 
// postorder traversal of the tree
void postorder(struct node* root)
{
    if (root == NULL)
    {
        return;
    }
 
    postorder(root->left);
    postorder(root->right);
    printf("%d ", root->data);
}

Output

------- AVL TREE --------
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
Enter Your Choice: 1
Enter data: 2
Do you want to continue? y

------- AVL TREE --------
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
Enter Your Choice: 1
Enter data: 2
Do you want to continue? y

------- AVL TREE --------
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT

Enter Your Choice: 3
Enter data: 2

 Node found

Do you want to continue? y


------- AVL TREE --------
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
Enter Your Choice: 2
Enter data: 2
Do you want to continue? y

------- AVL TREE --------
1. Insert
2. Delete
3. Search
4. Inorder
5. Preorder
6. Postorder
7. EXIT
Enter Your Choice: 4
2
Do you want to continue? n

Output2: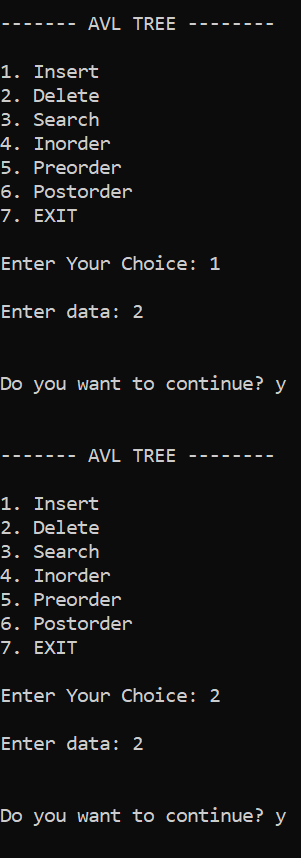

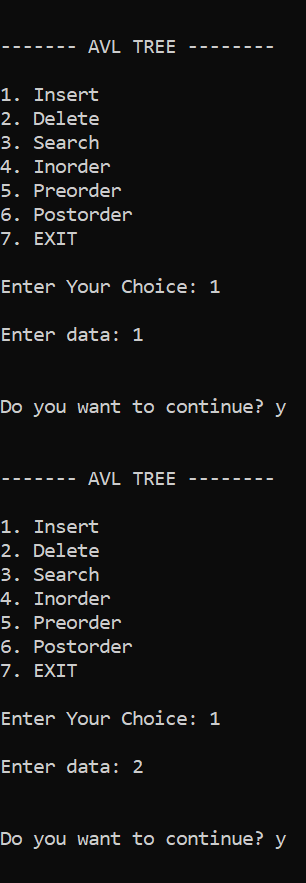
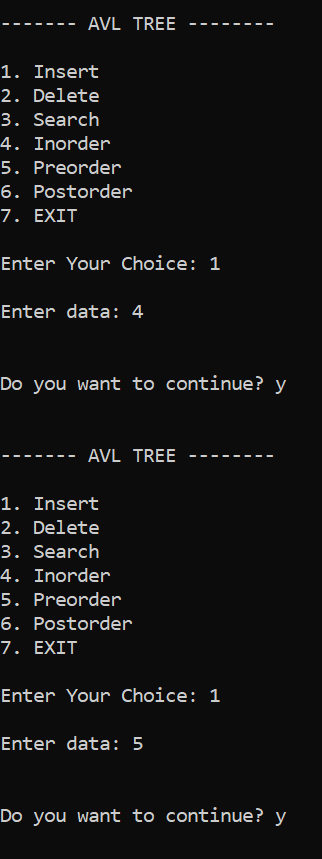
Conclusion:

The AVL tree's running time complexity for insertion operations is O(log n) for finding the place of insertion and returning to the root. Similar to this, determining the node to be deleted and carrying out the subsequent operations to change the AVL tree's balance factor have running time complexity of O(log n). Compared to the binary search tree, the AVL tree has a faster and more stable time complexity.

Next TopicB Tree Applications

← prev next →

For Videos Join Our Youtube Channel: Join Now

Feedback

Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Splunk

SPSS

Swagger

Transact-SQL

Tumblr

ReactJS

Regex

Reinforcement Learning

R Programming

RxJS

React Native

Python Design Patterns

Python Pillow

Python Turtle

Keras

Preparation

Aptitude

Reasoning

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Artificial Intelligence

AWS

Selenium

Cloud Computing

Hadoop

ReactJS

Data Science

Angular 7

Blockchain

Git

Machine Learning

DevOps

B.Tech / MCA

DBMS

Data Structures

DAA

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

Automata

C Programming

C++

Java

.Net

Python

Programs

Control System

Data Mining

Data Warehouse

Javatpoint Services

JavaTpoint offers too many high quality services. Mail us on h[email protected], to get more information about given services.

Website Designing
Website Development
Java Development
PHP Development
WordPress
Graphic Designing
Logo
Digital Marketing
On Page and Off Page SEO
PPC
Content Development
Corporate Training
Classroom and Online Training
Data Entry

Training For College Campus

JavaTpoint offers college campus training on Core Java, Advance Java, .Net, Android, Hadoop, PHP, Web Technology and Python. Please mail your requirement at [email protected].
Duration: 1 week to 2 week

^{Like/Subscribe us for latest updates or newsletter}

DS Tutorial

DS Array

DS Linked List

DS Stack

DS Queue

DS Tree

DS Graph

DS Searching

DS Sorting

Differences

Misc

DS MCQ

AVL Tree Program in C

What Is an AVL Tree?

Balance factor properties -

The AVL Tree's rotations:

Implementation:

Insertion procedures include the following steps:

AVL Tree Program in C

Conclusion:

Feedback

Help Others, Please Share

Learn Latest Tutorials

Preparation

Trending Technologies

B.Tech / MCA

Javatpoint Services

Training For College Campus