B Tree Applications
Traditional binary search trees have certain unpleasant limitations. Introducing the B-Tree, a versatile data structure that handles enormous quantities of data with ease. Due to their slow pace and large memory usage, traditional binary search trees may become impractical for storing and searching huge volumes of data.
B-Trees, often referred to as Balanced Trees or B-Trees, are a kind of self-balancing tree that was created expressly to get around these restrictions.
B-Trees, also known as "big key" trees, are distinguished from conventional binary search trees by the enormous number of keys that they can hold in a single node.
A B-Tree can have many keys at each node, which increases the branching factor and lowers the height of the tree. Because of the reduced disc I/O caused by this lower height, search and insertion operations are completed more quickly. Hard drives, flash memory, and CD-ROMs are examples of storage devices that benefit most from B-Trees because of their sluggish, clumsy data access.
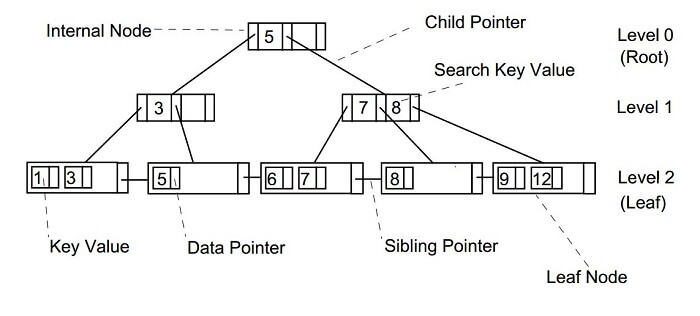
Each node in a B-Tree must have a minimum amount of keys in order for the tree to remain balanced.
This balance guarantees that the temporal complexity of operations like insertion, deletion, and searching is always O(log n) regardless of how the tree is initially constructed.
B-Tree Time Complexity:
| Sr. No. |
Algorithm to Implement |
Time Complexity |
| 1. |
To Search |
O(log n) |
| 2. |
To Insert |
O(log n) |
| 3. |
To Delete |
O(log n) |
Here, the total number of elements in the B-tree is 'n'.
B-Tree applications:
- Large databases employ it to access information stored on discs.
- Using the B-Tree, finding data in a data set can be done in a great deal less time.
- Multilevel indexing is possible with the indexing feature.
- The B-tree method is also used by the majority of servers.
- In CAD systems, B-Trees are used to catalogue and search geometric data.
- Other applications of B-Trees include encryption, computer networks, and natural language processing.
- Since accessing values stored in a large database that is stored on a disc takes a long time, B trees are used to index the data and provide quick access to the actual data stored on the disks.
- In the worst case, it takes O(n) running time to search a database with n key values that is not sorted or indexed. However, if we use B Tree to index this database, it will be searched in O (log n) time in worst case.
Advantages of B-Trees:
- B-Trees are well suited for big data sets and real-time applications because they have a guaranteed time complexity of O (log n) for fundamental operations like insertion, deletion, and searching.
- B-Trees can balance themselves.
- High throughput and concurrency.
- Efficient use of the storage space.
Disadvantages of B-Trees:
- They are dependent on disk-based data structures and can use a lot of disc space.
- Not always the greatest option.
- Comparatively slow to other data structures.
NOTE:
The B-smallest Tree's possible height when there are n nodes and m children (the most children a node can have) is:
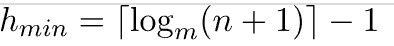
With n nodes and t being the smallest n umber of children, a non-root node can have, the greatest height of the B-Tree that can exist is:
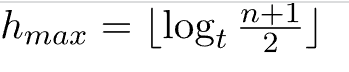
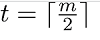
Origin of B Tree
- When brought into main memory (or RAM), data that has been saved on the disc in blocks is referred to as a data structure.
- Due to the large amount of data and frequent disc access, searching for a single record in a large volume of data necessitates reading the entire volume.
- To get around this, index tables that save the record references of the records based on the blocks they sit in are built. The amount of time and memory consumed is significantly decreased.
- We can develop multi-level index tables because we have a large amount of data.
- B Tree can be used to create multi-level indexes that keep the data sorted in a self-balancing way.
- B-Tree traversal is comparable to inorder Binary Tree traversal in terms of traversal. Starting with the leftmost child, we recursively print that child before doing the same for the keys and remaining children. At the end, recursively print the child on the right. A binary search tree and a B-tree both use similar search methods. The searchable key should be k.
- Recursively move up the tree, beginning at the root.
- If the non-leaf node has the key, we just return it for every visited node.
- If not, we go back to the node's proper child (the child that comes before the first greater key).
- If we arrive at a leaf node and k is not present there, return NULL.
- A binary tree search is similar to a B-Tree search. The algorithm uses recursion and is comparable. The search is optimized at each level so that if the key value is not present in the parent's range, it is present in a different branch. These numbers are also referred to as limiting values or separation values because they restrict the search. It will display NULL if we reach a leaf node and can't find the necessary key.
|

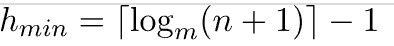
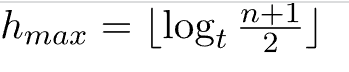
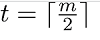
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now










