Binary AdderThe registers play an important role in performing the micro-operations. The registers hold the digital component and the data which performs the arithmetic operation. The Binary Adder is a logical circuit which is used to perform the addition operation of two binary number of any length. The Binary Adder is formed with the help of the Full-Adder circuit. The Full-Adders are connected in series, and the output carry of the first Adder will be treated as the input carry of the next Full-Adder. N-Bit Parallel AdderThe Full Adder is used to sum two single-bit binary numbers with carry input. In digital calculation, we need to add two n-bit binary numbers rather than only single-bit binary numbers. For this purpose, we need to use n-bit parallel Adder. In order to get N-bit parallel adder, we cascade the n number of Full Adders. The carry output of the first Adder is treated as the carry input of the second Adder. 4-bit Binary Adder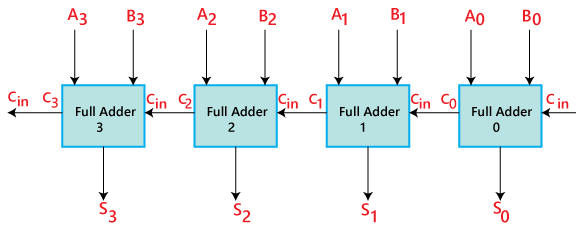
Next TopicBinary Adder-Subtractor
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










