Binary Search tree vs AVL tree

Before knowing about the Binary search tree and AVL tree differences, we should know about the binary search tree and AVL tree separately.

What is a Binary Search Tree?

The binary search tree is a tree data structure that follows the condition of the binary tree. As we know, that tree can have 'n' number of children, whereas; the binary tree can contain the utmost two children. So, the constraint of a binary tree is also followed by the binary search tree. Each node in a binary search tree should have the utmost two children; in other words, we can say that the binary search tree is a variant of the binary tree.

The binary search tree also follows the properties of the binary search. In binary search, all the elements in an array must be in sorted order. We calculate the middle element in the binary search in which the left part of the middle element contains the value lesser than the middle value, and the right part of the middle element contains the values greater than the middle value.

In Binary Search Tree, the middle element becomes the root node, the right part becomes the right subtree, and the left part becomes the left subtree. Therefore, we can say that the binary search tree is a combination of a binary tree and binary search.

Note: Binary Search Tree can be defined as the binary tree in which all the elements of the left subtree are less than the root node, and all the elements of the right subtree are greater than the root node.

Time Complexity in Binary Search Tree

If the binary search tree is almost a balanced tree then all the operations will have a time complexity of O(logn) because the search is divided either to the left or the right subtree.

If the binary search tree is either left or right-skewed, then all the operations will have the time complexity of O(n) because we need to traverse till the n elements.

What is the AVL Tree?

An AVL tree is a self-balancing binary search tree where the difference between heights of left and right subtrees cannot be more than one. This difference is known as a balance factor. In the AVL tree, the values of balance factor could be either -1, 0 or 1.

How does the self-balancing of the binary search tree happen?

As we know that AVL tree is a self-balancing binary search tree. If the binary search tree is not balanced, it can be self-balanced with some re-arrangements. These re-arrangements can be done using some rotations.

Let's understand self-balancing through an example.

Suppose we want to insert 10, 20, 30 in an AVL tree.

The following are the ways of inserting 10, 20, 30 in an AVL tree:

• If the order of insertion is 30, 20, 10.

Step 1: First, we create a Binary search tree, as shown below: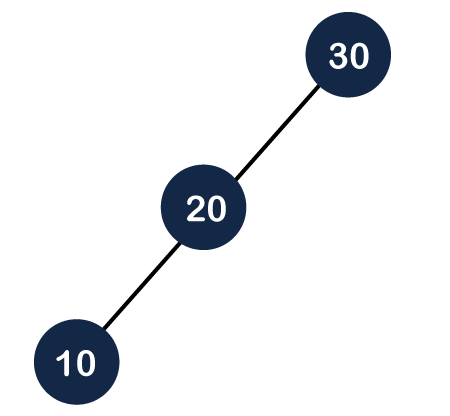

Step 2: In the above figure, we can observe that tree is unbalanced because the balance factor of node 30 is 2. In order to make it an AVL tree, we need to perform some rotations. If we perform the right rotation on node 20 then the node 30 will move downwards, whereas the node 20 will move upwards, as shown below: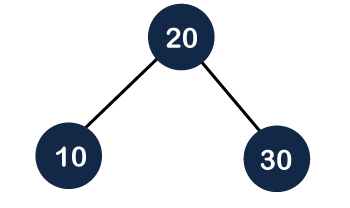

As we can observe, the final tree follows the property of the Binary Search tree and a balanced tree; therefore, it is an AVL tree.

In the case, the tree was left unbalanced tree, so we perform the right rotation on the node.

• If the order of insertion is 10, 20, 30.

Step 1: First we create a Binary search tree as shown below: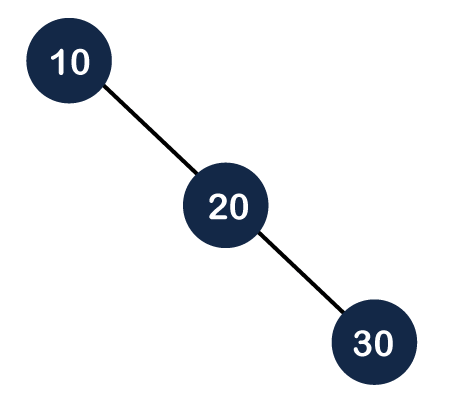

Step 2: In the above figure, we can observe that the tree is unbalanced because the balance factor of node 10 is -2. In order to make it an AVL tree, we need to perform some rotations. It is a right unbalanced tree, so we will perform left rotation. If we perform left rotation on node 20, then the node 20 will move upwards, and node 10 will move downwards, as shown below: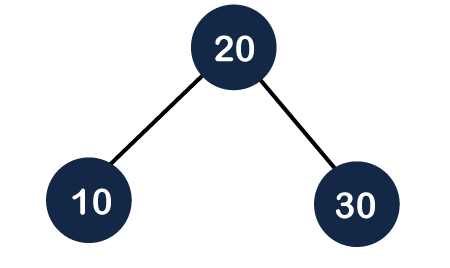

As we can observe, the final tree follows the property of the Binary Search tree and a balanced tree; therefore, it is an AVL tree.

• If the order of insertion is 30, 10, 20

Step 1: First we create the Binary Search tree as shown below: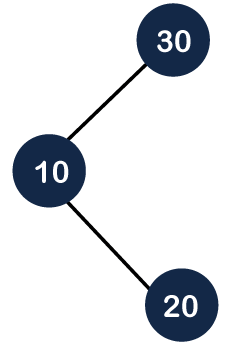

Step 2: In the above figure, we can observe that the tree is unbalanced because the balance factor of the root node is 2. In order to make it an AVL tree, we need to perform some rotations. The above scenario is left-right unbalanced as one node is the left of its parent node and another is the right of its parent node. First, we will perform the left rotation, and rotation happens between nodes 10 and 20. After left rotation, 20 will move upwards, and 10 will move downwards as shown below: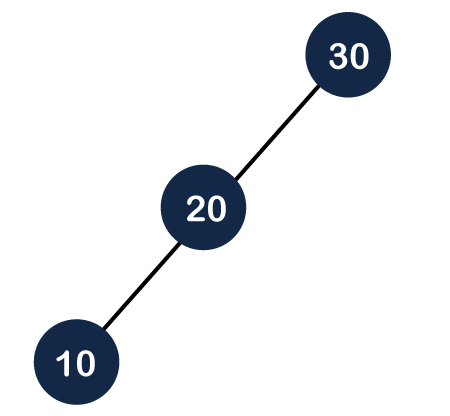

Still, the tree is unbalanced, so we perform the right rotation on the tree. Once the right rotation is performed on the tree, then the tree would like, as shown below: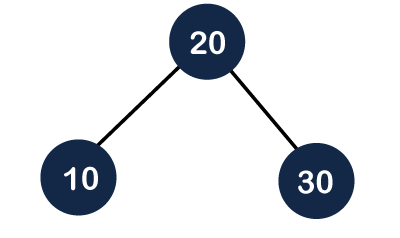

As we can observe in the above tree, the tree follows the property of the Binary Search tree and a balanced tree; therefore, it is an AVL tree.

• If the order of the insertion is 10, 30, 20

Step 1: First, we create the Binary Search tree, as shown below: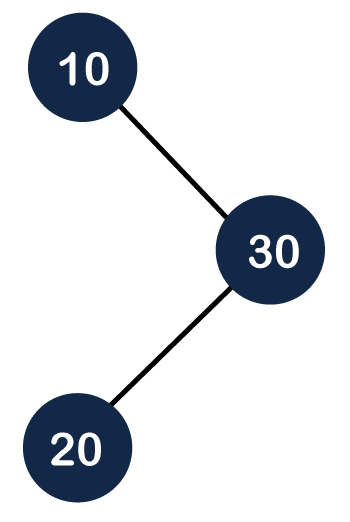

Step 2: In the above figure, we can observe that tree is unbalanced because the balance factor of the root node is 2. In order to make it an AVL tree, we need to perform some rotations. The above scenario is right-left unbalanced as one node is right of its parent node, and another node is left of its parent node. First, we will perform the right rotation that happens between nodes 30 and 20. After right rotation, 20 will move upwards, and 30 will move downwards as shown below: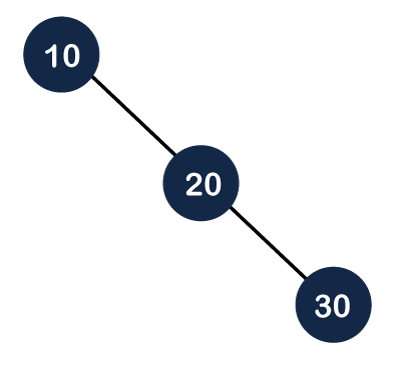

Still, the above tree is unbalanced, so we need to perform left rotation on the node. Once the left rotation is performed, the node 20 will move upwards, and node 10 will move downwards as shown below: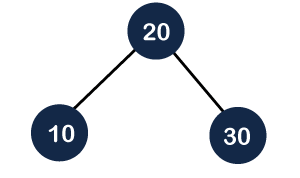

As we can observe in the above tree, the tree follows the property of the Binary Search tree and a balanced tree; therefore, it is an AVL tree.

Differences between Binary Search tree and AVL tree