Bipartite Graph in Discrete mathematics

If we want to learn the Euler graph, we have to know about the graph. The graph can be described as a collection of vertices, which are connected to each other with the help of a set of edges. In this section, we are able to learn about the definition of a bipartite graph, complete bipartite graph, chromatic number of a bipartite graph, its properties, and examples.

Definition of Bipartite graph

The bipartite graph can be described as a special type of graph which has the following properties:

• This graph always has two sets, X and Y, with the vertices.
• In this graph, the vertices of set X can only have a connection with the set Y.
• We cannot join the vertices within the same set.

The example of a Bipartite graph is described as follows:

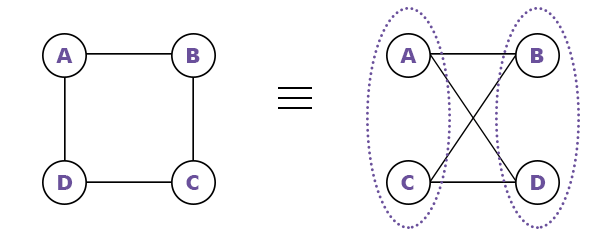
In the above graph, we have the following things:

• We can decompose the vertices of a given graph into two sets.
• The decomposed sets are set X = {A, C}, and set Y = {B, D}.
• The vertices of set X can only make a connection with set Y and vice versa.
• We cannot join the vertices of same set.
• Hence, the given graph is a bipartite graph.

Complete Bipartite graph

• We can define the bipartite graph in many ways. In other words, we can say that the complete bipartite graph has many definitions, which are described as follows:
• A graph will be known as the complete bipartite graph if every vertex of set X has a connection with every vertex of set Y.
• A graph will be called complete bipartite if it is bipartite and complete both.
• If there is a bipartite graph that is complete, then that graph will be called a complete bipartite graph.

Example of Complete Bipartite graph

The example of a complete bipartite graph is described as follows:

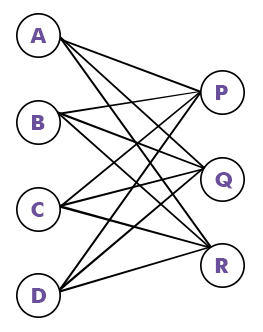
In the above graph, we have the following things:

• The above graph is a bipartite graph and also a complete graph.
• Therefore, we can call the above graph a complete bipartite graph.
• We can also call the above graph as k_{4, 3}.

Chromatic Number of Bipartite graph

When we want to properly color any bipartite graph, then we have to follow the following properties:

• For this, we have required a minimum of two colors.
• We have to use different colors to color the end vertices of every edge.
• In this case, the bipartite graphs will be 2 colorable.

Note: If there is no edge in the bipartite graph, then that graph will be 1 colorable.

Example of chromatic number of bipartite graph:

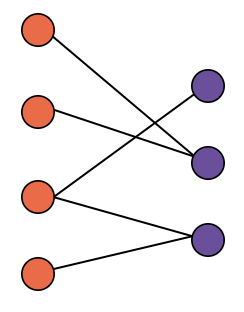
In the above bipartite graph, the chromatic number is 2 because the left side vertices are colored with orange color, and the right side vertices are colored with red color. So there are two colors. Hence, chromatic number = 2.

Properties of Bipartite graph

There are various properties of a bipartite graph, and some important properties are described as follows:

• The bipartite graphs are 2 colorable.
• There are no odd cycles in the bipartite graphs.
• If there is any sub-graph in the bipartite graph, then that subgraph will also be itself bipartite.
• If there is a case where |X| ≠ |Y|, then the bipartite graph will not contain a perfect match with the bipartition X and Y.
• If there is a bipartite graph that contains a bipartition X and Y, then it will have the following relation:
  

Perfect matching for a Bipartite Graph

In a bipartite graph, there is a formula for perfect matching, which is described as follows:

To understand this, we will assume that we have a bipartite graph G and its bipartition X and Y. Now we will show the cases for a perfect matching:

• If there is a case where |X| ≠ |Y|, then the bipartite graph will not have a perfect matching.
• If there is a case where a number of elements in the neighborhood of a subset are greater than or equal to all subsets of X and the number of elements in that subsets, in this case, the bipartite graph will contain the perfect matching with bipartition X and Y.

Maximum Number of Edges

• If there is any bipartite graph that has the n number of vertices, then that graph contains at most (1/4)*n² number of edges.
• In the bipartite graph, maximum possible number of edges on 'n' vertices is equal to the (1/4)*n².

Explanation:

• Suppose V1 and V2 are the bipartition of the graph where |V1| = k and |V2| = n - k.
• k(n-k) is at most number of edges between bipartition V1 and V2, and the edges can be maximized at k = n/2.
• Thus, there is a maximum 1/4 * n2 number of edges that can be present.
• The graph G will have a triangle if there is a graph G that contains n vertices and also have more than 1/4 * n2 edges.
• The bipartite graph does not have odd cycles. That's why it is not in this graph.

Examples of Bipartite Graph

There are various examples of bipartite graphs, and some of them are described as follows:

Example 1: In this example, we have to show whether the given graph is a bipartite graph or not.

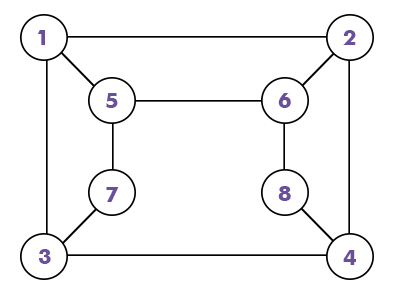
Solution:

We can draw the above graph in another way, which is described as follows:

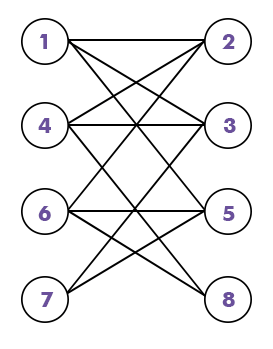
In the above redraw graph, we have the following things:

• In the above graph, we have two sets of vertices, i.e., X and Y.
• The set X = {1, 4, 6, 7} and Y = {2, 3, 5, 8}.
• In his graph, the vertices of set X only have a connection with the vertices of set Y, and the same happened with the set Y and set X.
• We cannot join the vertices of same set.
• All these properties satisfy the bipartite graph definition.

Hence, the above graph is known as the bipartite graph.

Example 2: In this example, we have 12 vertices of the bipartite graph, and we have to determine the maximum number of edges on that graph.

Solution: As we have learned above that, the maximum number of edges in any bipartite graph with n vertices = (1/4) * n²

Now we will put n = 12 in the above formula and get the following:

In a bipartite graph, the maximum number of edges on 12 vertices = (1/4) * (12)²

= (1/4) * 12 * 12

= 1/4 * 144

= 36

Hence, in the bipartite graph, the maximum number of edges on 12 vertices = 36.