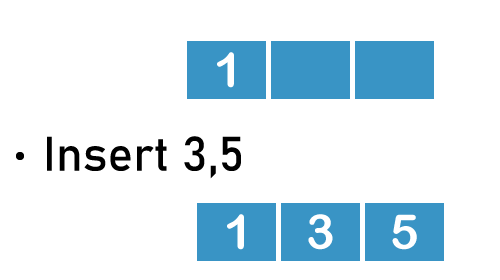B+ Tree Insertion

B-tree and B+ trees are typically used to achieve dynamic multilevel indexing. However, the disadvantage of the B-tree used for indexing is that it also keeps the data pointer (a pointer to the disc file block containing the key value), corresponding to a certain key value, in the B-tree node. This method significantly decreases the number of items that can fit inside a B-tree node, which leads to an increase in the B-level tree's structure and longer search times for records. By only storing data pointers at the tree's leaf nodes, the B+ tree gets rid of the above flaw.

As a result, the interior nodes of the B tree and the leaf nodes of a B+ tree have very distinct structures. It should be emphasized that since data pointers are only present at leaf nodes, all key values and their accompanying data pointers to the disc file block must be stored by leaf nodes in order for them to be accessible. Additionally, the leaf nodes are connected to offer organized access to the records. Therefore, the leaf nodes constitute the index's first level, with the internal nodes being the other levels in a multilevel index.

To only serve as a medium to regulate record searching, some of the leaf nodes' key values also appear in internal nodes. A B+ tree, unlike a B-tree, has two orders, "a" and "b," one for internal nodes and the other for external (or leaf) nodes. This is clear from the description above. An internal B+ tree of order "a" has the following node structure:

Each internal node has the following structure: where each Ki is a key-value pair, and each Pi is a tree pointer (pointing to another node of the tree) (see diagram-I for reference).
Each internal node contains the following values for each search field: K1 < K2 < …. < Kc-1
The following statement is true for each value of search field "X" in the Pi-pointed subtree: Ki-1 < X <= Ki, where1 < i < c and, Ki-1 < X.
At most 'a' tree pointer is present in each internal node.
The internal nodes each have at least ceil(a/2) tree pointers, while the root node has at least two tree pointers.
An internal node has 'c -1' key values if it has 'c' pointers, where c< = a.

If the values are stored in order, most queries can be processed more quickly. However, it is impractical to expect to store the table's rows in sorted order and one after the other as doing so would necessitate recreating the table for each row that is added or removed.

This prompts us to think of putting our rows in a tree structure instead. Our initial thought would be a balanced binary search tree, like a red-black tree, but since databases are kept on disc, this actually doesn't make much sense. Disks function by reading and writing large blocks of data all at once; these blocks are typically 512 bytes or four kilobytes in size. A little portion of that is used by each node in a binary search tree.

Finding a structure that fits more neatly inside a disc block makes sense.

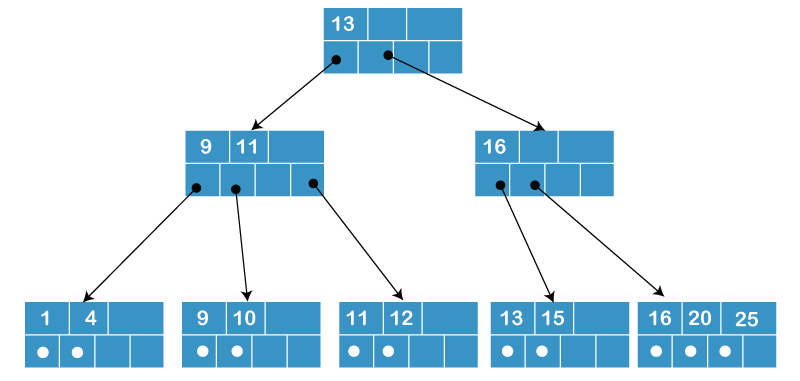
This results in the B+-tree, where each node contains up to d keys and up to d references to children. Each reference refers to the root of a subtree for which all values are between two of the node's keys and is therefore deemed to be "between" two of the node's keys.

Here is a somewhat small tree with the value 4 for d.

B+ Tree Characteristics

Only leaf nodes can store data points.
Keys are found in internal nodes.
We utilize keys in B+ trees to perform direct element searches.
There will be at least "[m/2] -1" keys and a maximum of "m-1" keys if there are "m" elements.
At least two children and one key are present in the root node.
Each node other than the root can have a minimum of "m/2" children and a maximum of "m" children for "m" elements.

Insertion on a B+ Tree

You will learn about insertion operations on a B+ tree in this tutorial. Additionally, working C, C++, Java, and Python examples of putting members into a B+ tree are provided.

There are three basic steps involved in adding an element to a B+ tree: finding the right leaf, adding the element, and balancing or breaking the tree.

Let's examine these occurrences in detail below.

Operation of Insertion

These characteristics need to be taken into consideration before adding an element to a B+ tree.
The root has a minimum of two children.
Each node, excluding the root, is allowed to have at least m/2 children and a maximum of m children.
A minimum of m/2 - 1 keys and a maximum of m - 1 keys can be found in each node.
The processes for inserting an element are as follows.
Go to the proper leaf node since each element is inserted into a leaf node.
Activate the leaf node with the key.

Case I

Insert the key into the leaf node in ascending order if the leaf is not fully extended.

Case II

If the leaf is filled, place the key in each leaf node in ascending order, then balance the tree as follows.
At the m/2 th position, break the node.
Additionally, add the m/2nd key to the parent node.
Follow steps two through three if the parent node is already full.

Example:

Show the tree after insertions.

Assume that each B+-tree node may store up to 4 pointers and 3 keys:

m=3 (odd), d=1
Partial (for odd m value)
A leaf node with at least two (d+1) entries
Non-leaf nodes with at least two (d+1) pointers and one entry
Insert 1, 3, 5, 7, and 9.
Insert 1
Insert 3, 5
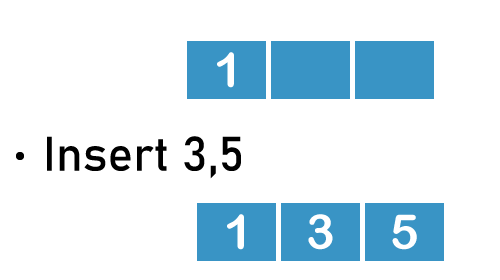
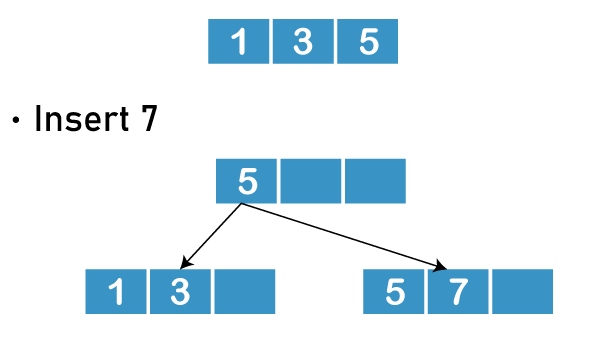
Insert 7
Insert 9

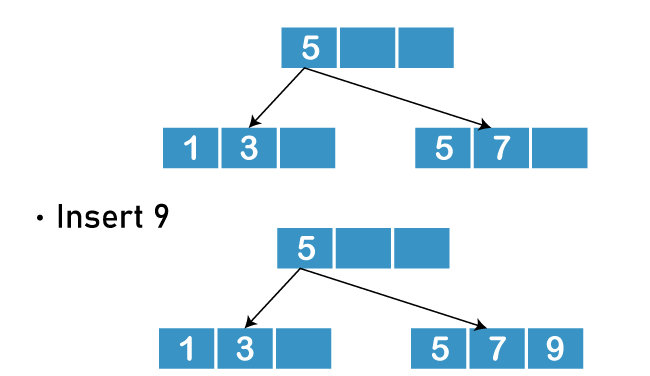
This is the final B+ Tree.

Program in C++:

Code:

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define pb push_back
 
int bucketSize = 3;
 
// Create 2 classes, one for node and one for tree;
 
class node {
public:
    bool isLeaf;
    node** ptr;
    int *key, size;
    node();
};
node::node()
{
    key = new int[bucketSize];
    ptr = new node*[bucketSize + 1];
}
class Btree {
public:
    // Root of tree stored here;
    node* root;
    Btree();
    void deleteNode(int);
 
    int search(int);
    void display(node*);
    void insert(int);
    node* findParent(node*, node*);
    node* getRoot();
    void shiftLevel(int, node*, node*);
};
 
node* Btree::getRoot() { return root; }
Btree::Btree() { root = NULL; }
 
void Btree::insert(int x)
{
    if (root == NULL) {
        root = new node;
        root->key[0] = x;
        root->isLeaf = true;
        root->size = 1;
    }
 
    else {
        node* current = root;
        node* parent;
 
        while (current->isLeaf == false) {
            parent = current;
 
            for (int i = 0; i < current->size; i++) {
                if (x < current->key[i]) {
                    current = current->ptr[i];
                    break;
                }
 
                if (i == current->size - 1) {
                    current = current->ptr[i + 1];
                    break;
                }
            }
        }
 
        // now we have reached leaf;
        if (current->size
            < bucketSize) { // if the node to be inserted is
                            // not filled
            int i = 0;
 
            // Traverse btree
            while (x > current->key[i] && i < current->size)
                // goto pt where needs to be inserted.
                i++;
 
            for (int j = current->size; j > i; j--)
                // adjust and insert element;
                current->key[j] = current->key[j - 1];
 
            current->key[i] = x;
 
            // size should be increased by 1
            current->size++;
 
            current->ptr[current->size]
                = current->ptr[current->size - 1];
            current->ptr[current->size - 1] = NULL;
        }
 
        // if block does not have enough space;
        else {
            node* newLeaf = new node;
            int tempNode[bucketSize + 1];
 
            for (int i = 0; i < bucketSize; i++)
                // all elements of this block stored
                tempNode[i] = current->key[i];
            int i = 0, j;
 
            // find the right posn of num to be inserted
            while (x > tempNode[i] && i < bucketSize)
                i++;
 
            for (int j = bucketSize + 1; j > i; j--)
                tempNode[j] = tempNode[j - 1];
            tempNode[i] = x;
            // inserted element in its rightful position;
 
            newLeaf->isLeaf = true;
            current->size = (bucketSize + 1) / 2;
            newLeaf->size
                = (bucketSize + 1)
                  - (bucketSize + 1)
                        / 2; // now rearrangement begins!
 
            current->ptr[current->size] = newLeaf;
            newLeaf->ptr[newLeaf->size]
                = current->ptr[bucketSize];
 
            current->ptr[newLeaf->size]
                = current->ptr[bucketSize];
            current->ptr[bucketSize] = NULL;
 
            for (int i = 0; i < current->size; i++)
                current->key[i] = tempNode[i];
 
            for (int i = 0, j = current->size;
                 i < newLeaf->size; i++, j++)
                newLeaf->key[i] = tempNode[j];
 
            // if this is root, then fine,
            // else we need to increase the height of tree;
            if (current == root) {
                node* newRoot = new node;
                newRoot->key[0] = newLeaf->key[0];
                newRoot->ptr[0] = current;
                newRoot->ptr[1] = newLeaf;
                newRoot->isLeaf = false;
                newRoot->size = 1;
                root = newRoot;
            }
            else
                shiftLevel(
                    newLeaf->key[0], parent,
                    newLeaf); // parent->original root
        }
    }
}
 
void Btree::shiftLevel(int x, node* current, node* child)
{ // insert or create an internal node;
    if (current->size
        < bucketSize) { // if can fit in this level, do that
        int i = 0;
        while (x > current->key[i] && i < current->size)
            i++;
        for (int j = current->size; j > i; j--)
            current->key[j] = current->key[j - 1];
 
        for (int j = current->size + 1; j > i + 1; j--)
            current->ptr[j] = current->ptr[j - 1];
 
        current->key[i] = x;
        current->size++;
        current->ptr[i + 1] = child;
    }
 
    // shift up
    else {
        node* newInternal = new node;
        int tempKey[bucketSize + 1];
        node* tempPtr[bucketSize + 2];
 
        for (int i = 0; i < bucketSize; i++)
            tempKey[i] = current->key[i];
 
        for (int i = 0; i < bucketSize + 1; i++)
            tempPtr[i] = current->ptr[i];
 
        int i = 0, j;
        while (x > tempKey[i] && i < bucketSize)
            i++;
 
        for (int j = bucketSize + 1; j > i; j--)
            tempKey[j] = tempKey[j - 1];
 
        tempKey[i] = x;
        for (int j = bucketSize + 2; j > i + 1; j--)
            tempPtr[j] = tempPtr[j - 1];
 
        tempPtr[i + 1] = child;
        newInternal->isLeaf = false;
        current->size = (bucketSize + 1) / 2;
 
        newInternal->size
            = bucketSize - (bucketSize + 1) / 2;
 
        for (int i = 0, j = current->size + 1;
             i < newInternal->size; i++, j++)
            newInternal->key[i] = tempKey[j];
 
        for (int i = 0, j = current->size + 1;
             i < newInternal->size + 1; i++, j++)
            newInternal->ptr[i] = tempPtr[j];
 
        if (current == root) {
            node* newRoot = new node;
            newRoot->key[0] = current->key[current->size];
            newRoot->ptr[0] = current;
            newRoot->ptr[1] = newInternal;
            newRoot->isLeaf = false;
            newRoot->size = 1;
            root = newRoot;
        }
 
        else
            shiftLevel(current->key[current->size],
                       findParent(root, current),
                       newInternal);
    }
}
int Btree::search(int x)
{
    if (root == NULL)
        return -1;
 
    else {
        node* current = root;
        while (current->isLeaf == false) {
            for (int i = 0; i < current->size; i++) {
                if (x < current->key[i]) {
                    current = current->ptr[i];
                    break;
                }
 
                if (i == current->size - 1) {
                    current = current->ptr[i + 1];
                    break;
                }
            }
        }
 
        for (int i = 0; i < current->size; i++) {
            if (current->key[i] == x) {
                // cout<<"Key found "<<endl;
                return 1;
                // return;
            }
        }
 
        // cout<<"Key not found"<<endl;
        return 0;
    }
}
 
// Print the tree
void Btree::display(node* current)
{
    if (current == NULL)
        return;
    queue<node*> q;
    q.push(current);
    while (!q.empty()) {
        int l;
        l = q.size();
 
        for (int i = 0; i < l; i++) {
            node* tNode = q.front();
            q.pop();
 
            for (int j = 0; j < tNode->size; j++)
                if (tNode != NULL)
                    cout << tNode->key[j] << " ";
 
            for (int j = 0; j < tNode->size + 1; j++)
                if (tNode->ptr[j] != NULL)
                    q.push(tNode->ptr[j]);
 
            cout << "\t";
        }
        cout << endl;
    }
}
 
node* Btree::findParent(node* current, node* child)
{
    node* parent;
    if (current->isLeaf || (current->ptr[0])->isLeaf)
        return NULL;
 
    for (int i = 0; i < current->size + 1; i++) {
        if (current->ptr[i] == child) {
            parent = current;
            return parent;
        }
        else {
            parent = findParent(current->ptr[i], child);
            if (parent != NULL)
                return parent;
        }
    }
    return parent;
}
 
signed main()
{
    ios_base::sync_with_stdio(false);
    Btree node;
    cout << "The size of bucket is " << bucketSize << "! "
         << endl;
 
    node.insert(1);
    node.insert(2);
    node.insert(3);
    node.display(node.getRoot());
    node.insert(4);
    node.insert(5);
    node.display(node.getRoot());
 
    return 0;
}

Output

The size of bucket is 3! 
1 2 3     
3     
1 2     3 4 5

Advantages of B+ Trees:

In comparison to a B-tree with the same number of levels, a B+ tree can store more entries in its internal nodes. This emphasizes how much the search time for every specific key has been improved. Because of their lower levels and Pnext pointers, B+ trees are particularly rapid and effective at accessing records from drives.
A B+ tree allows for both sequential and direct access to data.
To fetch records, an equivalent number of disc accesses are required.
Because of the redundant search keys in B+ trees, it is impossible to store search keys again.

Disadvantages of B+ Trees:

The difficulty of accessing the keys in a sequential manner is the main disadvantage of B-tree. The quick random access is still present in the B+ tree.

Application of B+ Trees:

Multiple Indexing
faster tree operations (insertion, deletion, search)
indexing a database

B Tree Vs B+ Tree

The following are some of the variations between B and B+ tree:

Data and search keys are kept in internal or leaf nodes in a B tree. Data, however, is only kept at leaf nodes of the B+ tree.
Because all data are located in leaf nodes of a B+ tree, searching for any data is incredibly simple. Data cannot be discovered in leaf nodes of a B tree.
Data can be located in internal nodes or leaf nodes of a B tree. Internal node deletion is highly challenging. Data only exists in leaf nodes of a B+ tree. Leaf node deletion is fairly simple because it can be directly deleted.
Insertion in B tree is more complicated than B+ tree.
B+ trees store redundant search key but B tree has no redundant value.
In a B+ tree, leaf nodes data are ordered as a sequential linked list but in B tree the leaf node cannot be stored using a linked list. Many database systems' implementations prefer the structural simplicity of a B+ tree.

The basic difference lies between how they make use of the internal storage.

Overview:

A B+ tree is a non-linear storage structure that stores a collection of data elements with a "one-to-many" relationship, typically used in databases and operating system file systems.

Non-leaf nodes do not store data, only indexes (redundant), and more indexes can be placed.
Leaf nodes contain all index fields.
Leaf nodes are linked with pointers to improve interval access performance.

Why B+ Tree?

Since MySQL usually stores data on disk, reading data will generate disk IO consumption. The non-leaf nodes of the B+ tree do not store data. Usually, the size of a node is set to the size of the disk page, so that each node of the B+ tree can put more keys, and the height of the B+ tree is lower, reducing disk IO consumption.
B+ tree leaf nodes form a linked list and use range search and sorting.

MySQL Uses B+ tree as An Index

Since MySQL usually stores data on disk, reading data will generate disk IO consumption. The non-leaf nodes of the B+ tree do not save data, but the non-leaf nodes of the B tree will save data. Usually, the size of a node will be set to the disk page size, so that each node of the B+ tree can hold more keys, while the B tree has more keys. few. As a result, the height of the B tree will be higher than that of the B+ tree, which will result in more disk IO consumption.
B+ tree leaf nodes form a linked list and use range search and sorting. The B-tree for range search and sorting requires recursive traversal of the tree.

Next TopicChecking for the Mirror Images in the Binary Trees

← prev next →