Brahmagupta

Brahmagupta was an Indian astronomer and mathematician who lived from 598 to 668 CE. He composed the philosophic book "Brahmasphutasiddhanta" and the "Khandakhadyaka", a considerably more practical instruction on science and mathematics. He was the very first mathematician to develop formulae for the area of a cyclic quadrilateral. His contributions to geometry are substantial.

Brahmagupta was the first person to provide guidelines for calculating with zero. Brahmagupta's works were written in elliptic verse in Sanskrit, as was usual in Indian maths.

Early Life

According to his statements in some received sources, Brahmagupta was born in 598 CE. He resided in Bhillamala, presently Bhinmal, in Rajasthan, although during reign of the Chavda dynasty ruler, Vyagrahamukha. He was always focused to work finding new concepts. Later, commentators referred to him as a Bhillamalacharya or the instructor from Bhillamala. Bhillamala was the capital of the Gurjaradesa, West India's second-biggest state, which comprised contemporary India 's south side Rajasthan & north side Gujarat. It was also a centre of study institutions for mathematics and astronomy.

Brahmagupta studied the five classic Siddhantas of Indian astronomy but also the learning of many other astronomers, including Aryabhata I, Latadeva, Pradyumna, Varahamihira, Simha, Srisena, Vijayanandin, and Vishnuchandra. Somewhere at the age of 30, he authored and introduced the book named Brahmasphutasiddhanta, which itself is regarded to be a revised version of the recognised Siddhanta of the Brahmapaksha institution of astronomy.

The book includes important math teachings, including algebra, geometry, trigonometry, and algorithmics, all of which are claimed to include new concepts credited to Brahmagupta himself. At the age of 67, he authored Khandakhadyaka, a practical handbook of Indian astronomy, categorized within Karana, for students.

Astronomy

Brahmagupta was harsh in his objections to competing astronomers, and his Brahmasphutasiddhanta represents one of the early internal divisions between many Indian mathematicians. Disputes in Brahmagupta's case originated mostly from the selection of scientific factors and ideas. The selection was more concerned with applying mathematics to the physical world to discover or understand new concepts.

Brahmagupta made a significant contribution to astronomy, including techniques for estimating the location of celestial bodies over a period, their emerging and setting, connectives, and the computation of lunar and solar eclipses.

Brahmagupta said that because the Moon is closer to the Ground than the sun, the degree of the lit section of the Moon is determined by the Sun's and Moon's relative positions, which can be calculated using the size of the separation between the two objects.

Algebra from Brahmagupta

In section eighteenth of Brahmasphutasiddhanta, Brahmagupta developed a solution to the generalized linear equation:

The difference between rupas remains unknown or unidentified within the given equation after it is inverted and/or divided by the output difference of the [coefficients] of the [unknowns]. The rupas are [subtracted on the side] below that from which the square and the unknown are to be subtracted.

It is typically an answer to the equation bx + c = dx + e. Here rupas denote the constant c and e. Moreover, the overall solution equals to below equation:

x= (e-c)/(b-d)

In addition, he provided two similar answers to the generic quadratic problem, which are solutions for the equation ax^2 + bx = c corresponding to,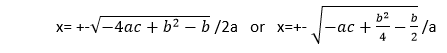

He answered processes of simultaneous indefinite equations first by isolating the chosen component but then just dividing the equation by the selected variable's coefficients.

Arithmetic

Many cultures including Brahmagupta were aware of the four fundamental functions of addition, subtraction, multiplication, and division. The present system relied on the Hindu-Arabic number system and was originally used in the Brahmasphutasiddhanta. Brahmagupta described the four different multiplication approaches in his book. One of those four approaches, named gom?trik?, is identical to present day's multiplication technique. In Middle Ages, Indian arithmetic was called modus Indorum, which translates as "Indian way."

Series

Brahmagupta also determined the combination of the squares and cubes of first n numbers. During this determination, Brahmagupta found the answer in terms of the sum of first n integers, instead of n, as is common nowadays.

Zero

The Brahmasphutasiddhanta of Brahmagupta was the very first publication to establish principles for mathematical operations with zero and negative integers. The Brahmasphutasiddhanta is considered the first recognized literature to regard zero as a figure in and of itself, instead of as a placeholder digit in expressing another number, as the Babylonians did, or as a sign for lack of amount, as Ptolemy and the Romans did.

Brahmagupta later defined that 0 / 0 = 0, meaning that when zero is divided from zero than it is equal to zero. But, he did not explain the equation a / 0 where a≠ 0. However, he stated that if any type of value (numeric) is divided by zero, it yields the total zero.

Achievements of Brahmagupta

Brahmagupta discovered the qualities of the digit 0, which became critical for the development of math and science. Brahmagupta listed the features of zero as follows:

• If we subtract a number from its own, we receive a zero.
• When zero is divided from zero than it is equal to zero.
• Any type of value (numeric) is divided by zero yields the total zero.

Following are some other notable achievements of Brahmagupta:

• Found a method for solving quadratic equations.
• Almost accurately calculated the value of pi (3.162). Brahmagupta increased the value by 0.66 per cent over the actual worth (3.14).
• He calculated that the Earth is closer to the Moon than the Sun.
• A formula for calculating the area of any 4-side figure whose edges touch from inside a circle was discovered.
• A year is 365 days, 6 hours, 12 minutes, and 9 seconds long.
• Brahmagupta mentioned 'gravity'. 'Bodies fall toward the earth because it is in the fact that the earth to attract bodies, just as it is in the nature of water to flow,' he said.
• The Earth is a sphere whose circumference is approximately 36,000 km, which means 22,500 miles.

His greatest notable piece, Brahmasphutasiddhanta, was composed in 628 CE when he was around 30 years old. This book contains twenty-five sections and 1008 stanzas. Historians believe that Brahmagupta wrote only the first 10 sections because they are organized according to astronomy texts from the time.

He wrote the following rules:

1. Debt is a debt even after subtracted from zero.
2. A fortune is a fortune even after subtracted from zero.
3. Zero subtraction from zero equals zero.
4. A debt subtracts from zero is a fortune.
5. Debt is a fortune deducted from zero.
6. Zero multiplied by a debt or fortune equals zero.
7. The product of zero multiplied by zero is 0.
8. One fortune is the product or quotient of two fortunes.
9. One fortune is the product or quotient of two debts.
10. Debt is the product or quotient of a debt and a fortune.

Death

It is believed that Brahmagupta died between the year 660 and 670 CE. Many sources have stated that he lived till 668 CE. He is regarded as one of the greatest Indian mathematicians of all time. His efforts in mathematics and science have made significant distinctions to many mathematical problems by creating the fundamental rules that now allow us to solve most problems.

BRAHMASPHUTASIDDHANTA

• One of Brahmagupta's most valuable contributions to mathematics was the introduction of the number 'zero' into the numerical system. It meant 'none.'
• The 'Brahmasphutasiddhanta,' which included numerous other mathematical findings expressed in poetry, is most probably the earliest known literature to consider nil as a quantity with its own right. It had several arithmetic rules, which are now used in calculations.
• He also gave the value of 'Pi' and considered 3 as the practical significance of Pi (π).
• In addition, he introduced the idea of negative values.
• The majority of his significant discoveries were written in the form of poems instead of mathematical formulas. Despite this, facts are facts, no matter how it is written.
• Following that, journalist Prithudaka Swami referred him as Bhillamalacharya, which translates as "the teacher from Bhillamala".

Sources of Historic Mathematics

When examining a math background, it is important to know the characters and where they originated. The origins of Mesopotamian and Egyptian mathematics may be traced back to scribe-written ancient documents. Although there are just several files in the case of Egypt, they are all of the same types and leave no doubt that Egyptian mathematics was elementary and deeply practical in its orientation, on the whole.

The newspaper has primarily addressed the difficulty of accessing safe texts in contemporary times, enabling historians of mathematics to concentrate their edit attempts on mathematicians' interactions or unpublished works.

Historians devised a mechanism for estimating these texts for adding mathematical growth and adding pertinent variables. The information was then organised into a table that identified locations much further ahead as the recorder wished. The Babylonians' sexagesimal technique provides significantly larger computing power than was required for the previous problem writings.

The parts of this system owned the Greeks for a very short period. It was carried down through the Greeks to Arab scholars throughout the Middle Ages and then to Europe, where it was influential in mathematical astronomy during the Renaissance and early modern periods.

Books

Khandakhadyaka

Khandakhadyaka is an astronomy book authored in 665 AD by Indian mathematician and astrologer Brahmagupta. The work is divided into eight chapters that address themes such as planet longitudes, diurnal rotation, lunar and solar eclipses, risings and sets, the Moon's crescent, and planet conjunctions. The treatise also includes an appendix, which comprises 1 chapter inside some editions and three in others.

Brahmasphutasiddhanta

The Brahmasphutasiddhanta is Brahmagupta's principal work, written around 628. This mathematical, astronomical book includes important mathematical content, such as a decent understanding of the role of nil, guidelines for manipulating both negative and positive numbers, a method for calculating square roots, methods for tackling linear and quadratic equations, and guidelines for summing series, Brahmagupta's identity, and Brahmagupta's theorem.

Later Year

• He is thought to have spent just a few years living and working in Bhinmal, Rajasthan, India. He excelled as an astronomer in the intellectual climate of the city, which was a centre of learning for mathematics and astronomy.
• He initially computed a year to be Three sixty-five days, six hours, five minutes, and nineteen seconds, which is extremely close to the correct value of three sixty-five days, five hours, forty-eight minutes, and forty-five seconds.
• In addition to presenting two comparable solutions to the generic quadratic equation, he developed novel approaches to solving quadratic equations and provided formulas to resolve systems of simultaneous indeterminate equations.
• His impact on geometry was extremely noteworthy in maths. His cyclic quadrilateral formula, now known as Brahmagupta's formula, calculates the area of any cyclic quadrilateral given the lengths of the sides.
• Brahmagupta was mostly known for working on mathematical and astronomical issues and sometimes mixing the two. Brahmagupta's explanations of celestial and planetary movements were based on mathematical computations that previous astronomers had not accomplished.

The Mysterious Life of Brahmagupta

The few existing records about him emphasize his mathematics and scientific accomplishments. We know that Brahmagupta was born in 598 CE in Bhillamala, India's Gurjaradesa area.

India was among the first and most productive traditional civilizations to engage with celestial and planetary motions. Ancient astronomers utilized simple equipment like a sun prism or the like of a contemporary sundial to solve extremely complicated equations that determined the positions of celestial planets.

Toward the end of his life, Bhramagupta relocated to Ujjain, where he authored his final major texts, the Khandakhadyaka and the Grahanarkajnana, at age 67.

Brahmagupta trained as an astronomer, learning from famous Indian scientists and writings. He additionally learned the 5 basic Siddhantas on astronomy.

Why is Zero Important?

Zero (0) has an important role in mathematics. Although it seems like a nill value without any meaning, it can have a big impact in any mathematical calculation and change the output. While it may appear obvious that '0' is a number and we can generate it by subtracting a value from itself. Also, dividing zero by zero returns 0.

The great mathematicians of Greek Culture, who were ahead of their time in several instances, had not made this discovery. Nobody else had unless Brahmagupta came up with this concept.

Many findings came together to develop the idea of zero. The round number sign and the notion of describing orders of magnitude in a number by using places emerged at different periods and locations prior to Brahmagupta's work.