Bubble Sort in JavaScript

What is Bubble Sort?

Sorting is the technique of shuffling the given array into increasing or decreasing order. There are various techniques or algorithms available to sort the array, like the bubble sort, insertion sort, merge sort, quick sort, radix sort etc.

Bubble sort is the most popular sorting algorithm. We are given an array of integers, and we have to sort the given array using a bubble sort algorithm.

Algorithm

In this algorithm, we create the bubble of two adjacent elements, and we move this bubble from starting to the ending of the array.

We will create the whole process maximum n times where n is the total number of elements in the array.

In this algorithm, we will compare two adjacent elements, and if the smaller index value is greater than the larger index value, then we will swap these two values and move to the next two adjacent values.

In one pass of the array, we will put one maximum element at its correct position. So maximum, we needed n pass or n iteration of this comparison.

For example: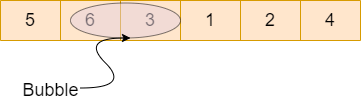

In the above example :

For i=0

For j=0

arr[j]<arr[j+1] ,so no swap and array = [5,6,3,1,2,4]

For j=1

arr[j]>arr[j+1] so we will swap these values and array = [5,3,6,1,2,4]

For j=2

arr[j]>arr[j+1] so we will swap these values and array = [5,3,1,6,2,4]

For j=3

arr[j]>arr[j+1] so we will swap these values and array = [5,3,1,2,6,4]

For j=4

arr[j]>arr[j+1] so we will swap these values and array = [5,3,1,2,4,6]

After i=0 array is [5,3,1,2,4,6]

Now for i=1

For j=0

arr[j]>arr[j+1] so we will swap these values and array = [3,5,1,2,4,6]

For j=1

arr[j]>arr[j+1] so we will swap these values and array = [3,1,5,2,4,6]

For j=2

arr[j]>arr[j+1] so we will swap these values and array = [3,1,2,5,4,6]

For j=3

arr[j]>arr[j+1] so we will swap these values and array = [3,1,2,4,5,6]

For j=4

arr[j]<arr[j+1] ,so no swap and array = [3,1,2,4,5,6]

After i=1 array is = [3,1,2,4,5,6]

For i=2

For j=0

arr[j]>arr[j+1] so we will swap these values and array = [1,3,2,4,5,6]

For j=1

arr[j]>arr[j+1] so we will swap these values and array = [1,2,3,4,5,6]

For j=2

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=3

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=4

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

After i=2 array is = [1,2,3,4,5,6]

For i=3

For j=0

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=1

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=2

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=3

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=4

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

After i=3 array is = [1,2,3,4,5,6]

For i=4

For j=0

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=1

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=2

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=3

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=4

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

After i=4 array is = [1,2,3,4,5,6]

For i=5

For j=0

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=1

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=2

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=3

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

For j=4

arr[j]>arr[j+1] so no swap and array = [1,2,3,4,5,6]

Javascript code:

Output:

Time complexity: O(N²), where N is the total number of elements in the array.

Space complexity: O(1)

Note: If the array is already sorted, we should check for further iterations. If the complexity increases, we can reduce it.

For example, after i=2 array was sorted, we checked until i=5, which increased our complexity. So we will use flag variables to reduce the time complexity and reduce the number of iterations.

Javascript code:

Output:

Time complexity: O(N2), where N is the total number of elements in the array.

Space complexity: O(1)

Note: If there are zero swaps for any i, then it means the array is sorted so that we will break the loop.