Capacitance Definition

The capacity of a material object or equipment to store an electric charge is referred to as capacitance. It is quantified as the ratio of the charge change to the difference in electric potential. Mutual capacitance & self-capacitance are two capacitance concepts that are well-understood. Electric potential between a charged object as well as the ground can be used to measure the self-capacitance of electrically chargeable things. When two components are measured for mutual capacitance, a fundamental linear electronic component used to increase capacitance in an electric circuit, the capacitor's function becomes very critical.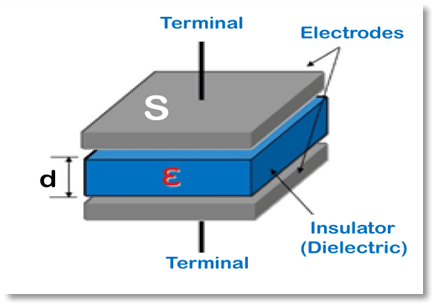

The only factors affecting the capacitance across two conductors are their geometry, distance from one another, opposing surface areas, and the permittivity of any dielectric substance in between. The capacitance & permittivity of many dielectric materials are independent of the total charge of the conductors and also the potential difference among them. The SI unit of capacitance is called a farad (symbol: F), after English physicist Michael Faraday. A 1-farad capacitor with a 1-coulomb electrical charge has a potential difference between its plates of 1 volt. Elastance is the name for capacitance's reciprocal.

Internal capacitance

The relative capacitance between two adjoining conductors, like that between the two plates of a capacitor, is typically referred to as capacitance when discussing electrical circuits. Every isolated conductor does, however, also display self-capacitance, a type of capacitance. It is calculated by the amount of electrical charge required to elevate the electric potential of an isolated conductor by a unit of measurement, say as one volt. The potential is defined as the point at which the conductor is centered inside a hollow conductive sphere with an infinite radius.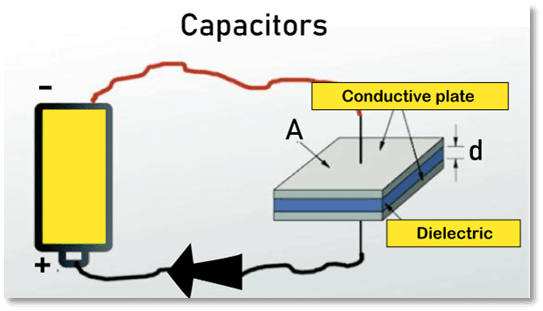

Capacitance measurement

An electronic test tool called a capacitance meter is used to measure capacitance, mostly in discrete capacitors. For most applications and situations, the capacitor must always be removed from the circuit.

Digital volt meters, or DVMs, frequently incorporate a capacitance-measuring feature. They typically work by applying a known current to charge and discharge the test capacitor while monitoring the rate at which the voltage rises; the slower the rate of rise, the greater the capacitance. Wider ranges are not uncommon, but DVMs typically only detect capacitance between nanofarads and a few hundred microfarads. Another method of determining capacitance is to apply a known high-frequency alternating current to the device being tested and then gauge the voltage that results (does not work for polarised capacitors).

Other methods are used by more advanced equipment, such as connecting the capacitor under test to a bridge circuit. The unknown capacitor's value is discovered by adjusting the other bridge legs' values (in order to make the bridge balanced). This indirect capacitance measurement technique guarantees greater accuracy. These devices can often measure capacitors across a range from picofarads to farads because of the use of Kelvin connections and other meticulous design methods.

Random capacitance

Any two neighbouring conductors can act as a capacitor, albeit the capacitance is typically low until the wires are near one another over a wide region or for extended periods of time. The term "parasitic" or "stray capacitance" refers to this capacitance. Stray capacitance can prevent circuits from operating properly at high frequencies by allowing signals to leak through normally isolated circuits (a phenomenon known as crosstalk).

Capacitors

Many orders of magnitude less capacitance than the farad are typically found in most capacitors for use in electronic circuits. The microfarad (F), nanofarad (nF), picofarads (pF), and femtofarad (fF) are the most popular subunits of capacitance used today. Although parasitic capacitive components can be as small as a femtofarad, specially designed super capacitors can be substantially bigger (up to hundreds of farads).

If the conductor geometry and the insulator's dielectric characteristics are known, it is possible to compute the capacitance. The following provides a qualitative explanation for this. In order to increase the required voltage, a positive charge must first be applied to a conductor. This positive charge then forms an electrical field that repels any more positive charges from being applied to the conductor. But, if a neighbouring conductor has a negative charge, the electrical field of the positive conductor, which repels the second positive charge is weaker. So, because of the second conductor's negative charge, it is simpler to apply a positive charge to the first conductor, which is already positive, and vice versa; as a result, the required voltage is reduced.