Carnot engineCarnot engine is a theoretical engine whose working is based on the Carnot cycle, which comprises of four different stages. These stages describe the processes of conversion of the heat into work. Carnot also states that the engine requires a hot body, which acts as an energy source for the engine. It transfers that energy to the cold body in order to do some mechanical work. The concept of the heat transfer is based on the second law of thermodynamics. Here, we will discuss the history, energy stages of the Carnot engine, efficiency, Carnot's theorem, example of the Carnot engine, Carnot's cycle, and more. As stated, the Carnot engine has a direct relationship with the second law of thermodynamics. Let's first discuss the second law of thermodynamics. Second law of thermodynamicsThe second law of thermodynamics states that a thermodynamic variable named entropy (S) exists in the thermodynamic (a branch of physics) system. The change in the entropy S is defined as the ratio of the change in the heat transfer and the temperature. It is given by: 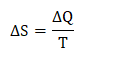
We can also say that the second law of thermodynamics defines quality of the energy. Let's consider two examples. Example 1: If a body at 100 degree Celsius is kept in contact with a similar body at 0 degree Celsius, the heat will start flowing from the body with higher temperature to the body with lower temperature. It means that the heat will flow from the hotter body to the colder body with both the bodies reaching at 50 degree Celsius. Example 2: Let a container be divided into two parts. One part is filled with gas and the other party is in vacuum (means no gas). When the valve between two reservoirs in a container is opened, the gas will start flowing towards the vacuum space till the gas eventually occupies both the parts of a container. Both the example depicts the second law of thermodynamics. Let's begin with the Carnot engine. Here, we will discuss the history, efficiency of a Carnot engine, Carnot's theorem, Carnot cycle, and more. History
Energy stages of Carnot EngineThere are four stages that describe the process of a Carnot engine. The graph describing such process is shown below: 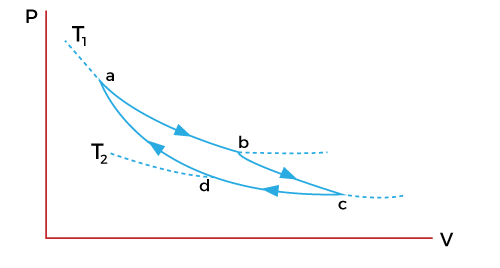
The schematic representation of the four states is shown below: 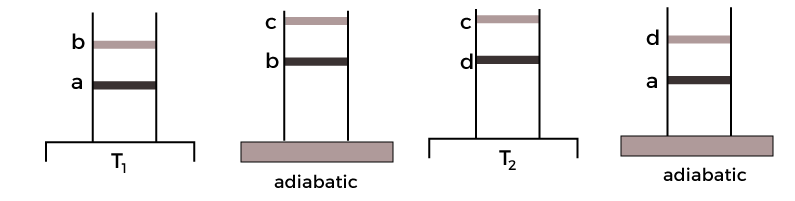
Let define the states with the help of an example. Suppose a cylinder is kept with a body at high temperature T1. At first, the body is in contact with the cylinder in a compressed state, which is represented as state 'a' in the above graph. The state 'b' represents the isothermal expansion of the gas. Work is done and the heat is supplied to the body at a specific temperature. Let the heat supplied, and the temperature be Q1 and T1. The cylinder is kept on the adiabatic platform and allows to expand. It has now reached the stage 'c'. The temperature at this stage starts falling from T1 to T2. The cylinder is now in contact with the lower temperature body due to the fall in the temperature at the 'c' stage. It is said to be isothermally compressed to the 'd' stage, as shown in the above graph. Work is done on the gas and it rejects the amount of heat (Q2) to the body at the temperature T2. It is now kept on the adiabatic platform and further compressed to reach the stage 'a'. The temperature at the stage 'a' is T1. The cyclic process 'abcda' is represent and explained above. The process can also be a reversible cyclic process if the piston is friction free and always moves slowly. Efficiency of a Carnot engineThe basic process of a Carnot engine is shown in the below diagram: 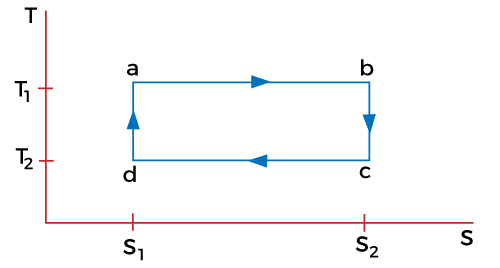
It represents the pressure-Volume diagram. Here, T represents the temperature and S represents the entropy. The points a, b, c, and d on the graph represent the states, as discussed above. Let the entropy in the state be S1. In the isothermal process ad, the amount of heat supplied to the system is Q1 at the temperature T1. As the heat is applied to the system, entropy increases, which is given by: S2 - S1 = Q1/T1 ...(1) The entropy in the bc and ad remains constant due to the adiabatic processes, as explained in the energy states. The entropy in state 'c' is S2. We know that the system gives heat Q2 in the part 'cd' at a lower temperature T2. The entropy at the stage 'd' thus reduces. The entropy in part 'da' remains constant due to the adiabatic process. Since, the entropy in stage 'a' is S1, it will be the same in the stage 'd' as well. Using the formula of the change in entropy, the process 'cd' can be represented as: S1 - S2 = -Q2/T2 ...(2) It is because S2 is the decreases entropy as compared to S1. We can also write it as: S2 - S1 = Q2/T2 Comparing equation 1 and 2, we get: Q1/T1 = Q2/T2 Or Q2/Q1 = T2/T1 The efficiency of the Carnot engine is defined as work done divided by the energy. Efficiency = W/Q1 Work done is the change in energy in the process cd. Efficiency = Q1 - Q2 / Q1 = 1 - Q2/Q1 = 1 - T2/T1 Thus, we can say that the efficiency of the engine depends only on the temperatures of the hot and cold bodies. These are the two bodies between which the engine works. Carnot's theoremAs discussed, the Carnot engine is based on the second law of thermodynamics. It is a reversible type of engine, which is an efficient engine as compared to other types of heat engine. It means that the reversible engine operating between the same two temperatures have equal efficiency. No other engines operating between the same two temperatures have efficiency greater than the reversible type of heat engines. The above theorem is known as Carnot's theorem. It is given by: N = 1 - T2/T1 Example of a Carnot engineLet's discuss a daily life example of a Carnot engine, i.e., refrigerator. A heat pump is present in the refrigerator that carries out the process. The role of the heat engine is to use the heat from the body to convert it into work done and rejects the rest to the cold body. The refrigerator works in an opposite way as of heat engine. The heat pump present in the refrigerator passes the heat from the cold body and delivers it to the hot body. It takes an amount of heat from the cold body, processes it (work done) and supply the total energy to the heated body, which is in the form of heat. We can also notice that the surroundings around the refrigerator is quite hotter. The process of the refrigerator is shown below: 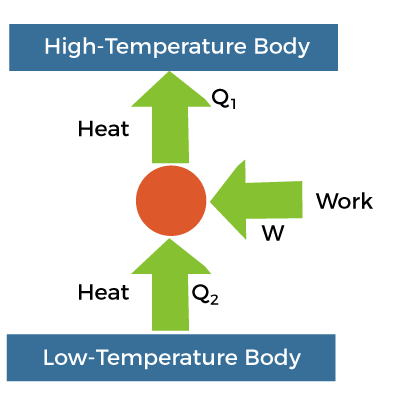
Carnot cycleA cycle occurs when a system is taken through the series of various states. One state of a cycle is linked to the other state. The last of the cycle again returns to the initial state. The process goes on and a cycle is formed. Here, the system might work on the surroundings (the area around the engine), acting as a heat engine. The Carnot's cycle is shown below: 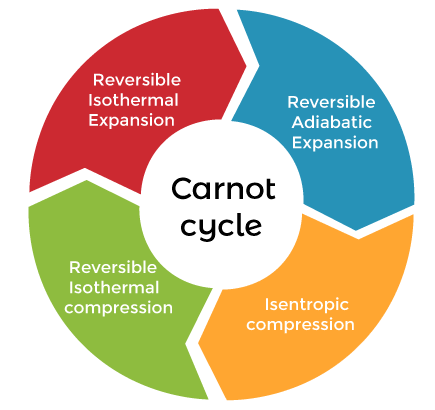
The Carnot cycle consists of the following steps:
Let's consider an example that depicts the function of different stages in the Carnot cycle. Here, we have assumed two reservoirs, and a free gap between the two reservoirs with a movable piston. The two reservoirs are cold reservoir and the hot reservoir. The expansion and compression of the piston will help us to determine the motion of the gas. The diagram is shown below: 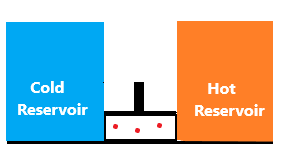
Reversible isothermal expansionHere, the piston is allowed to expand in the upper direction. The gas from the hot reservoir will move towards the piston area. The amount of heat absorbed by the piston area from the hot reservoir at a temperature is T1. 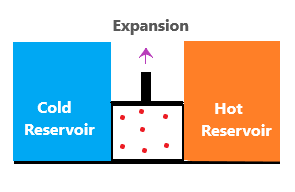
It is called reversible because the heat is transferred reversibly from the high reservoir at the content temperature. It is called isothermal because there is no change in temperature as the gas is in thermal contact with the reservoir. Reversible adiabatic expansionHere, the gas is insulated from both the reservoirs. Hence, there is no gain and lose of the heat energy, i.e., adiabatic. The gas continues to expand until some work is done due to the reduction of pressure. It loses energy due to the internal work done by the gas. The temperature at this stage is lower than the temperature T1, i.e., Ta. Reversible isothermal compressionThe gas is now in thermal contact with the low temperature reservoir (cold). The surroundings perform the work done on gas by compressing the piston. It causes the system to lose energy (Q2) to the cold reservoir. It further decreases the entropy of the system. Isentropic compressionIsentropic refers to the reverse adiabatic process. Here also, both the reservoirs are thermally insulated. The surrounding works on the gas and moves the piston further down. Such compression increases the internal energy of the system and the temperature again rises of T1, the same temperature in the first stage (reversible isothermal expansion). The entropy of the system remains unchanged. The stage 4 (isentropic compression) will now appear as the image shown below: 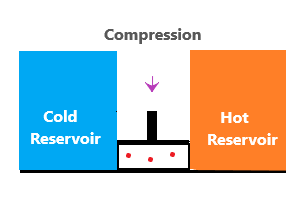
Advantages of the Carnot's engineThe advantages of the Carnot's engine are as follows:
Disadvantages of the Carnot's engineThe disadvantages of the Carnot's engine are as follows:
Applications of the Carnot engineThere are various applications of Carnot engine because it only requires the temperature gradient to perform the process. For example, steam engine, heat engine, etc. NumericalLet's consider a numerical example based on the Carnot engine. Example: A thermodynamic system is taken through the cycle abcda. Calculate the work done by the gas during different parts of the cycle, as shown in Figure 1. Also find the total heat rejected by the gas during the process. 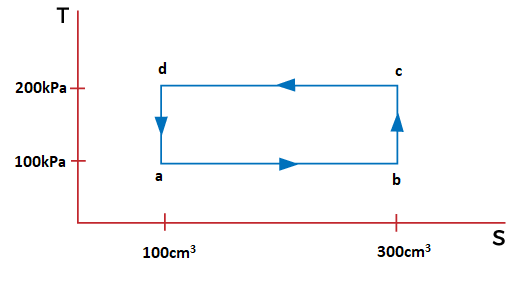
Solution: We know that the above cycle is represented in the graph form of p-V, where p is the pressure with the unit of Kilo Pascals and V is the volume with the unit Centimeter cubic. Here, we need to find the work done during the parts ab, bc, cd, and da. Step 1: Work done during the part ab It is given by: 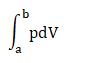
Where, p is the pressure V is the volume a represents the volume of 100cm3 and b represents the volume of 300cm3. Work done = 100kPa (300 - 100) cm3 = 100 x 1000 x 200 Pa cm3 = 20000000/1000000 Pa m3 It is because 1 m = 100 cm = 20 J Thus, the work done during the part ab is 20 Joules. Step 2: Work done during the part bc There is no change in the state in the part bc. The integration units (volume) will be the same, resulting in the zero work done. Thus, the work done during the part ab is 0 Joules. Step 3: Work done during the part cd It is given by: 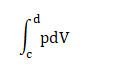
Where, p is the pressure V is the volume c represents the volume of 300cm3 and d represents the volume of 100cm3. Work done = 200kPa (100 - 300) cm3 =- 200 x 1000 x 200 Pa cm3 = -40000000/1000000 Pa m3 It is because 1 m = 100 cm = -40 J Thus, the work done during the part cd is -40 Joules. Step 4: Work done during the part da There is no change in the state in the part da. The integration units (volume) will be the same, resulting in the zero work done. Thus, the work done during the part cd is 0 Joules. Total heat rejected The total heat rejected is equal to the total work done by the system during the cycle abcda = 20 J - 40 J = - 20 Joules
Next TopicUnit of Heat
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










