Check if n and its Double Exist or not in Java

It is a problem frequently asked in interviews of top IT companies like Google, Amazon, TCS, HCL, IBM, and Accenture, etc. By solving the problem, one wants to check the logical ability, critical thinking, and problem-solving skill of the interviewee. So, in this section, we are going to find original array from a doubled array in Java with different approaches and logic. Also, we will create Java programs for the same.

Problem Statement

In this problem, an array that contains n elements is provided to us. Our task is to find an element in the array whose double also exists in the array. Mathematically, a[i] = 2 * a[j], such that i < n, and j < n, where n is the size of the input array. Note that i may or may not be equal to j.

Let's understand it through examples.

Example 1:

Input: numArr[] = {17, 11, 34, 10, 4, 9, 45}

Output: There exists an element in the input array whose double exists.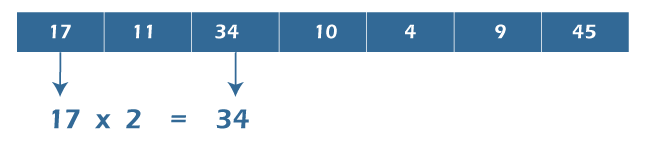

Check if n and its Double Exist or not in Java

Explanation: Consider the first and the third element of the input array, and we find that numArr[2] = 2 * numArr[0], i.e., 34 = 2 * 17.

Example 2:

Input: numArr[] = {7, 1, 3, 10, 4, 9, 15}

Output: There is no element in the input array whose double exists.

Example 3:

Input: numArr[] = {7, 1, 3, 0, 4, 9, 5}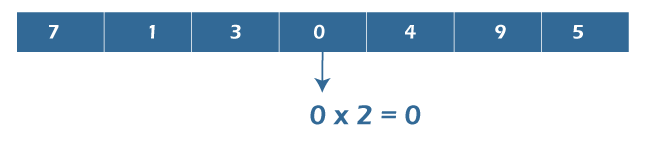

Output: There exists an element in the input array whose double exists.

Explanation: Consider the fourth element of the array, and we find that arr[3] = 2 * arr[3], i.e, 0 = 2 * 0.

Naive Approach

The straightforward or the naive approach is to check every element one by one and, for that element, iterate through the input array to find out whether its twice exists or not. It will be done with the help of two nested loops.

Algorithm

Step 1: Start a loop from j = 0 to n, where n is the total number of elements. Check whether numArr[j] = 0 or not. If it is 0, then return true. If it is not 0, enter in the inner loop (mentioned in step 2).

Step 2: Start another loop from k = j + 1 to n. In each iteration of the loop check the condition numArr[j] == 2 * numArr[k] or 2 * numArr[j] == numArr[k] is true or not. If it is true, an element exists whose twice also exists in the same array, and the loops can be terminated right there. If the condition is not true, then go to the next iteration, and check the condition again. Do the same for the other iterations too. If the outer loop terminates, then no element exists whose twice is available in the input array.

Let's implement the above algorithm in a Java program.

Java Program to Check if n and Its Double Exist or Not

FileName: DoubleEle.java

public class DoubleEle 
{
boolean isDoubleAvailable(int numArr[], int size)
{

for(int j = 0; j < size; j++)
{
if(numArr[j] == 0)
{
return true;
}

for(int k = j + 1; k < size; k++)
{
// either the jth element has to be twice of the kth element
// or the kth element has to be twice of the jth element, then only
// we can say that the double exists
if((numArr[j] == (2 * numArr[k])) || ((2 * numArr[j]) == numArr[k]))
{
    return true;
}
}


}

// if the control reaches here, it means double of any element does not exist
// hence, return false.
return false;

} 



// main method
public static void main(String argvs[])
{
// creating an object of the class DoubleEle
DoubleEle obj = new DoubleEle();
// input array
int numArr[] = {17, 11, 34, 10, 4, 9, 45};
// computing its size
int size = numArr.length;
// invoking the method isDoubleAvailable() and storing the answer
boolean ans = obj.isDoubleAvailable(numArr, size);
System.out.println("For the input array: ");
for(int i = 0; i < size; i++)
{
System.out.print(numArr[i] + " ");    
}
System.out.println();
if(ans)
{
System.out.print("There exists an element in the array whose double exists.");
}
else
{
System.out.print("There is no any element in the array whose double exists.");    
}

System.out.println("\n");

// input array
int numArr1[] = {7, 1, 3, 10, 4, 9, 15};

// computing its size
size = numArr1.length;

// invoking the method isDoubleAvailable() and storing the answer
ans = obj.isDoubleAvailable(numArr1, size);

System.out.println("For the input array: ");

for(int i = 0; i < size; i++)
{
System.out.print(numArr1[i] + " ");    
}
System.out.println();

if(ans)
{
System.out.print("There exists an element in the array whose double exists.");
}
else
{
System.out.print("There is no any element in the array whose double exists.");    
}

System.out.println("\n");

// input array
int numArr2[] = {7, 1, 3, 0, 4, 9, 5};
// computing its size
size = numArr1.length;
// invoking the method isDoubleAvailable() and storing the answer
ans = obj.isDoubleAvailable(numArr2, size);
System.out.println("For the input array: ");
for(int i = 0; i < size; i++)
{
System.out.print(numArr2[i] + " ");    
}
System.out.println();
if(ans)
{
System.out.print("There exists an element in the array whose double exists.");
}
else
{
System.out.print("There is no any element in the array whose double exists.");    
}
}
}

Output:

For the input array: 
17 11 34 10 4 9 45 
There exists an element in the array whose double exists.

For the input array: 
7 1 3 10 4 9 15 
There is no any element in the array whose double exists.

For the input array: 
7 1 3 0 4 9 5 
There exists an element in the array whose double exists.

Complexity Analysis: We have used nested for-loops for computing the answer. Hence, the time complexity of the program is O(n²), where n is the total number of elements present in the input array. Also, we have not used any data structure for keeping the results. Thus the space complexity of the program is constant, i.e., O(1).

Binary Search Approach

In this approach, we will be using the binary search to find the double of an element. The binary search approach will be more optimized than the previous approach.

Algorithm

Step 1: Sort the input array.

Step 2: Start a loop from i = 0 to n.

Step 3: For each iteration, pick the element pointed by the loop variable i, and store it in a variable, which is currEle in our case.

Step 4: Double the value of currEle and search this doubled value in the sorted array using binary search.

If the doubled value is found, then there exists an element whose double is present in the array, and we can exit from the loop.
Otherwise, repeat step 3 for other iterations. If all the iterations of the loop are exhausted, then there is no element whose double is present in the input array.

Let's implement the above algorithm in a Java program.

FileName: DoubleEle1.java

// important import statement
import java.util.Arrays;

public class DoubleEle1 
{
boolean findDouble(int numArr[], int left, int right, int find)
{

// applying binary search
while(left <= right)
{
    int mid = (left + right) / 2;
    if(numArr[mid] == find)
    {
        return true;
    }
    else if(numArr[mid] > find)
    {
        right = mid - 1;
    }
    else
    {
        left = mid + 1;
    }
}

// if the control reaches here, it means double of any element does not exist
// hence, return false.
return false;

}


boolean isDoubleAvailable(int numArr[], int size)
{
int left = 0;
int right = size - 1;

Arrays.sort(numArr);

for(int i = 0; i < size; i++)
{
int currEle = numArr[i];
if(findDouble(numArr, left, right, 2 * currEle))
{
// if the control reaches here, then it means
// at least one number is there whose double exists
// hence, there is no need to proceed further and 
// we can return true
return true;
}
}

return false;
}


// main method
public static void main(String argvs[])
{
// creating an object of the class DoubleEle1
DoubleEle1 obj = new DoubleEle1();

// input array
int numArr[] = {17, 11, 34, 10, 4, 9, 45};

// computing its size
int size = numArr.length;

// invoking the method isDoubleAvailable() and storing the answer
boolean ans = obj.isDoubleAvailable(numArr, size);

System.out.println("For the input array: ");

for(int i = 0; i < size; i++)
{
System.out.print(numArr[i] + " ");    
}
System.out.println();

if(ans)
{
System.out.print("There exists an element in the array whose double exists.");
}
else
{
System.out.print("There is no any element in the array whose double exists.");    
}

System.out.println("\n");

// input array
int numArr1[] = {7, 1, 3, 10, 4, 9, 15};

// computing its size
size = numArr1.length;

// invoking the method isDoubleAvailable() and storing the answer
ans = obj.isDoubleAvailable(numArr1, size);

System.out.println("For the input array: ");

for(int i = 0; i < size; i++)
{
System.out.print(numArr1[i] + " ");    
}
System.out.println();

if(ans)
{
System.out.print("There exists an element in the array whose double exists.");
}
else
{
System.out.print("There is no any element in the array whose double exists.");    
}

System.out.println("\n");

// input array
int numArr2[] = {7, 1, 3, 0, 4, 9, 5};

// computing its size
size = numArr1.length;

// invoking the method isDoubleAvailable() and storing the answer
ans = obj.isDoubleAvailable(numArr2, size);

System.out.println("For the input array: ");

for(int i = 0; i < size; i++)
{
System.out.print(numArr2[i] + " ");    
}
System.out.println();

if(ans)
{
System.out.print("There exists an element in the array whose double exists.");
}
else
{
System.out.print("There is no any element in the array whose double exists.");    
}


}

}

Output:

For the input array: 
17 11 34 10 4 9 45 
There exists an element in the array whose double exists.

For the input array: 
7 1 3 10 4 9 15 
There is no any element in the array whose double exists.

For the input array: 
7 1 3 0 4 9 5 
There exists an element in the array whose double exists.

Complexity Analysis: We have used a loop for picking an element, and the loop takes O(n) time. Also, for each iteration, we have used the binary search that takes O(log(n) time. Thus, the total time complexity of the above program is O(n * log(n)), where n is the total number of elements present in the array. Note that sorting also takes O(n * log(n)) time. However, the binary search operation and the sorting operation are not nested. Hence, the total time complexity of the program still remains the same. The program is taking constant space. Therefore, the total space complexity of the above program is O(1).

Approach: Using HashSet

In this approach, we will be storing the elements one by one in the HashSet. Using the method contains, we will check whether the double of an element exists or not.

Algorithm

Step 1: Check the first element of the input array. If it is zero, we are done, and there is no need to proceed further. Else go to the next step.

Step 2: Create a hash set and insert the first element of the input array.

Step 3: Start a loop from i = 1 to n, where n is the total number of elements present in the array.

Step 4: Check whether twice the number pointed by the loop variable i or half the number pointed by variable i is present in the hash set or not.

If present, we can say that at least one number is present in the array whose double is also available, and true can be returned.
Else, check whether the number pointed by variable i is 0 or not. If 0, return true.
Else, add the number in the hash set and go to the next iteration and repeat this step. If all the iterations of the loop are exhausted, then it means there is no element in the array whose double exists. Hence, false is returned.

Let's implement the above algorithm in a Java program.

FileName: DoubleEle2.java

// important import statement
import java.util.*;

public class DoubleEle2
{

boolean isDoubleAvailable(int numArr[], int size)
{
HashSet<Integer> hs = new HashSet<Integer>();
if(numArr[0] == 0)
{
    return true;
}
hs.add(numArr[0]);
for(int i = 1; i < size; i++)
{
// if twice of a number is present, we can return true
if(hs.contains(2 * numArr[i]))
{
return true;
}


// if the half of a number is present we have to ensure that
// the number is even
if(numArr[i] % 2 == 0 && hs.contains(numArr[i] / 2))
{
return true;
}

// if the number is zero, we can return true
if(numArr[i] == 0)
{
return true;
}

// add the number and move to the next iteration
hs.add(numArr[i]);
}

return false;

}


// main method
public static void main(String argvs[])
{
// creating an object of the class DoubleEle2
DoubleEle2 obj = new DoubleEle2();

// input array
int numArr[] = {17, 11, 34, 10, 4, 9, 45};

// computing its size
int size = numArr.length;

// invoking the method isDoubleAvailable() and storing the answer
boolean ans = obj.isDoubleAvailable(numArr, size);

System.out.println("For the input array: ");

for(int i = 0; i < size; i++)
{
System.out.print(numArr[i] + " ");    
}
System.out.println();

if(ans)
{
System.out.print("There exists an element in the array whose double exists.");
}
else
{
System.out.print("There is no any element in the array whose double exists.");    
}

System.out.println("\n");

// input array
int numArr1[] = {7, 1, 3, 10, 4, 9, 15};

// computing its size
size = numArr1.length;

// invoking the method isDoubleAvailable() and storing the answer
ans = obj.isDoubleAvailable(numArr1, size);

System.out.println("For the input array: ");

for(int i = 0; i < size; i++)
{
System.out.print(numArr1[i] + " ");    
}
System.out.println();

if(ans)
{
System.out.print("There exists an element in the array whose double exists.");
}
else
{
System.out.print("There is no any element in the array whose double exists.");    
}

System.out.println("\n");

// input array
int numArr2[] = {7, 1, 3, 0, 4, 9, 5};

// computing its size
size = numArr1.length;

// invoking the method isDoubleAvailable() and storing the answer
ans = obj.isDoubleAvailable(numArr2, size);

System.out.println("For the input array: ");

for(int i = 0; i < size; i++)
{
System.out.print(numArr2[i] + " ");    
}
System.out.println();

if(ans)
{
System.out.print("There exists an element in the array whose double exists.");
}
else
{
System.out.print("There is no any element in the array whose double exists.");    
}


}

}

Output:

For the input array: 
17 11 34 10 4 9 45 
There exists an element in the array whose double exists.

For the input array: 
7 1 3 10 4 9 15 
There is no any element in the array whose double exists.

For the input array: 
7 1 3 0 4 9 5 
There exists an element in the array whose double exists.

Complexity Analysis: We are using only one loop. Therefore, the time complexity of the above program is O(n), where n is the total number of elements present in the array. Since we have used the data structure hash set for storing the elements, therefore, the total space complexity of the program is O(1).

Next TopicArray of Doubled Pair Problem in Java

← prev next →