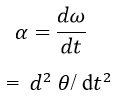Circular Motion Definition

It is a movement of a body while rotating along a circular path. Circular motion can be either uniform or non-uniform. The speed and angular rotation rate will be constant in the uniform circular motion, and in the non-uniform motion, the rotation rate will keep varying.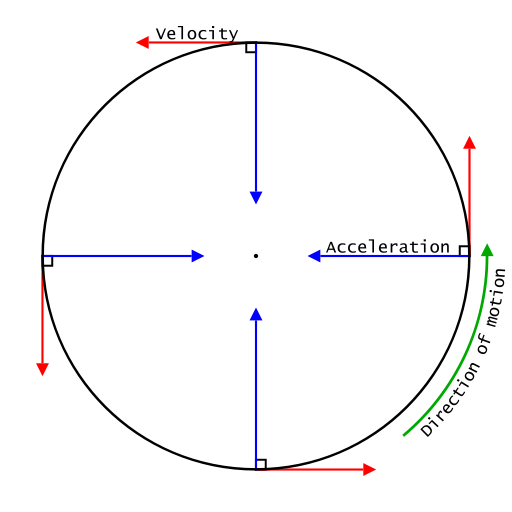

Some simple examples of circular motion include a moving car's wheel, gears in gas turbines, a rotating ceiling fan, and windmill blades.

A particle is said to be moving in a circular motion when it travels along the circumference of a circular path. An important aspect of circular motion is that the direction of the body in circular motion keeps varying. This is not the case in linear motion. Circular motion can also be represented in terms of angular variables.

Angular Displacement

Angular displacement is the angle made by moving particles per unit of time. It is denoted by ?? and calculated in the radians.

Angular Velocity

Angular velocity is defined as the rate of change in the angular displacement of a body in a circular motion. It is represented by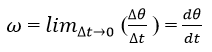

Angular velocity is calculated in radians/second.

Relationship Between the Linear Speed (V) and Angular Speed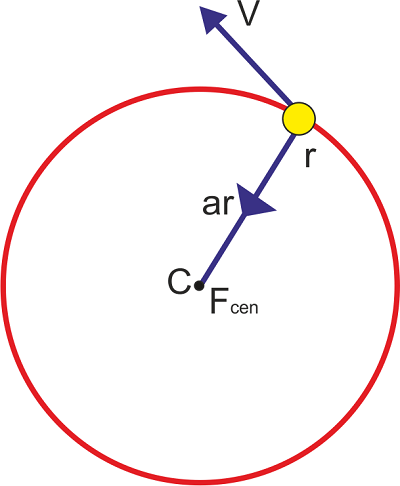

v = ω × r

Here, r represents the particle's position vector concerning the circle's centre.

v = rω

It has two components when the Acceleration of a particle is in a circular motion:

• Tangential Acceleration: It is the component of Acceleration acting in the direction of the particle's velocity.
  at= dv / dt
• Radial Acceleration: It is the acceleration component acting towards the circle's centre. This component initiates changes in the direction of the velocity of an object in a circular motion.
  ar = v²/r = rω².
• Angular Acceleration: It is the rate of change of angular velocity of a rotating object. Radian/ is used to measure it.
  

Circular motion is uniformed, and non-uniform is greatly dependent upon the nature of the Acceleration of the object.

Uniform Circular Motion: The motion is considered uniform when the object rotates along a circular path at a constant speed.

The velocity vector changes its position at each point in the circle. This meant that the radial component of the Acceleration always remained zero. The tangential component of the circle can assume a negative and positive value in the non-uniform circular motion, and zero values occur in the uniform circular motion.

We are aware of the fact that the Acceleration of the object in a circular motion acts towards the centre of the circle, and v is produced by / r. Using Newton's second law of motion in this case,

F_cen = mv²/ r

Here

m= mass of the object

F_c= Centripetal force acting towards the centre of the circle

Some examples of centripetal force include the tension in a string, gravitational force and Friction.

Newton's Laws of Motion Application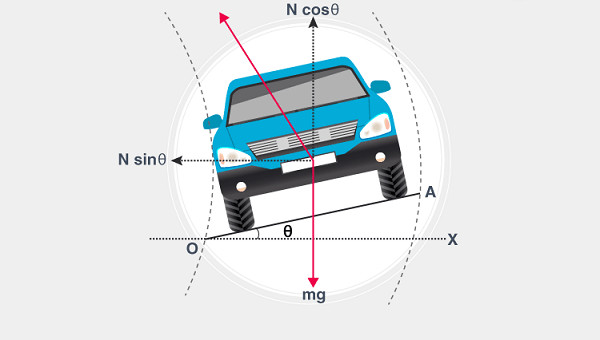

Usage of Newton's laws of motion in two different cases.

Case 1: At Level Road

What happens when a vehicle makes an instant turn on a level road? Three different forces will be acting in that case.

1. Normal Reaction N
2. The weight of the car W = mg
3. The Frictional Force

Since Normal reaction and the weight of the car is in the vertical direction,

N = Mg

N - mg = 0

Static Friction acts in the Centripetal Acceleration of an object moving in a circular direction. The static Friction resists the vehicle from getting away from the circle

f_r = mv² / r ≤ μN

Here μ denotes the coefficient of static Friction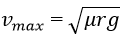

It implies the maximum possible speed of the object for the circular path of a given radius and .

Case 2: When the Roads are Banked

The friction effect on the motion of an object on a circular road can be reduced if the Road is slightly raised on the outer end of the Road. It is referred to as banking.

Assume that Road is banked at an angle and it has been illustrated in the figure:

The net force acting in the vertical direction is Zero, as there is the absence of Acceleration and direction

So,

NCosθ = f sinθ + mg ……………………………… (1)

The centripetal force acting by the horizontal component of N and f are

Frequently Asked Questions

Question: Determine the angular velocity of an object in the circular orbit, moving at a speed of 200 times per minute.

Answer: Given Quantity:

Frequency of rotation = 200 times/ minute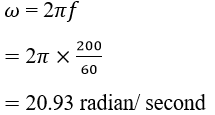

Question: An electric supported wheel is moving on its axis at the speed of 900 rotations/ minute. When the power was switched off, it took 1 minute to come to rest. Determine the angular deceleration of the wheel in radians per second.

Answer: Applying laws of motion in the rotational motion,

Question: A truck travels in a circular road of radius 1000, with a speed of 10m/s. A pendulum is suspended from the bus's roof by a rod of length 100cm. Determine the angle made by the rod with the Road.

Answer: Given the information

Speed of the truck = 10m/s

The radius of the circular Road = 1000 cm

Length of the rod = 100 cm

We know the formula,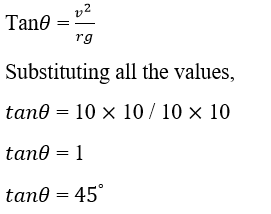

Question: Which option is untrue for a moving object in a circle with a uniform angular speed?

1. The velocity and acceleration vectors are perpendicular to each other
2. The velocity vector is tangent to the circle
3. The acceleration vector points to the centre of the circle
4. The acceleration vector is tangent to the circle

Answer: d.

Question: What is circular motion?

Ans: The motion of a body in a circular length along the perimeter of the circle or rotating along a circular path is called circular motion.

Question: What are the different forms of Circular motion?

Answer: The different forms of circular motion are:

• Non-Uniform Circular Motion
• Uniform Circular Motion

Question: Illustrate some examples of circular motion.

Ans: Examples of the circular motion include:

• Vehicles moving in a circular track
• Rotation of satellite in a circular orbit
• Ice skater skating in a circle

Question: Find the value of the instantaneous Acceleration in the Uniform circular motion.

Ans: The instantaneous Acceleration of the uniform circular motion

Here, v denotes the velocity of the object.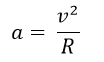

R denotes the radius of the circle.

The direction is perpendicular to the velocity and acts inwards through the radius.