Compound InterestIn mathematics, the calculation of compound interest is done on the principal amount and the interest accumulated over the previous period. It differs from simple interest (SI) because interest is not added to the principal amount. Compound interest is used in the financial and banking sector. It's some other applications are, increase or decrease in population and rise or depreciation in the value of an item. In this section, we will learn compound interest definition, formula, and how to calculate compound interest. Compound Interest DefinitionCompound interest is the addition of interest to the principal amount of a loan or deposit. In simple words, it is interest on interest. Compound interest is contrasted with simple interest. In the simple interest, the previously accumulated interest is not added to the principal amount of the current period, so there is no compounding. It is denoted by CI. The simple annual interest rate is the interest amount per period, multiplied by the number of periods per year. The simple annual interest rate is also known as the nominal interest rate. Compound Interest FormulaTo calculate the compound interest manually, we use formula. While calculating the CI amount and principal must be known. The CI is the difference of amount and principal amount. The formula of compound interest is given below.
Compound Interest (C.I.)=Amount (A)-Principal (P)
To calculate the amount, multiply the principal amount by one plus the rate of interest divide by the number of times interest applied raised to the number of compound periods minus one. The formula for calculating the amount is given below: 
Where: A: is the total amount after n years (Future amount) P: is the initial principal amount r: is the interest rate n: number of times interest applied per time period t: is the number of time periods elapsed Note: The above formula is the general formula for the number of times the principal is compounded in a year.
Where: A: is the total amount after t years (Future amount) P: is the initial principal amount r: is the interest rate t: is the number years money is invested Difference Between Compound Interest and Simple InterestThere are two types of interest compound and simple interest. Both types of interest grow money over a specified period. But they have a major difference. The main difference between SI and CI is that the simple interest is paid on the principal amount while the compound interest is paid on the principal plus interest that we have earned previously.
Let's solve some examples based on the above formulas. Example 1: What will be the compound interest on Rs. 4,000 in two years when the rate of interest is 5% per annum? Solution: Given, principal amount (P)=Rs.4,000 According to the formula: 
Putting the values in the formula, we get: 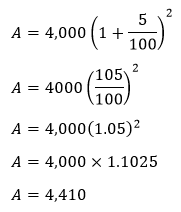
It is the amount after two years including the interest. We know that:
Compound Interest (C.I.)=Amount (A)-Principal (P)
Putting the values in the above formula, we get: C.I.=4,410-4,000 Hence, the compound interest is Rs. 410. Example 2: Amit borrowed a loan from the bank for Rs. 8,00,000. The bank has charged an interest of 7% per annum. Amit will return money to the bank after three years. Calculate the compound interest. Solution: Given, principal amount (P)=Rs.8,00,000 
Putting the values in the formula, we get: 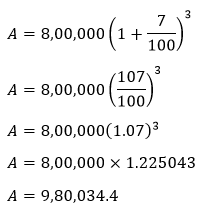
We know that:
Compound Interest (C.I.)=Amount (A)-Principal (P)
Putting the values in the above formula, we get: C.I.=9,80,034.4-8,00,000 Hence, the compound interest is Rs. 1,80,034.4. Example 3: Calculate the compound interest on Rs. 57,000 at the rate of 9% per annum compounded quarterly. Solution: Given, principal amount (P)=Rs.57,000 According to the formula, when interest is compounded quarterly: 
Putting the values in the formula, we get: 
We know that:
Compound Interest (C.I.)=Amount (A)-Principal (P)
Putting the values in the above formula, we get: C.I.=62,301-57,000 Hence, the compound interest is Rs. 5,301. Example 4: Priya deposited Rs. 1,22,000 in the bank. The bank paid her 12% interest per annum compounded quarterly. Calculate the amount that she gets after 9 months. Solution: Given, principal amount (P)=Rs.1,22,000 Rate of interest (r)=12%= Time (t)= 9 months=9/3 years=3 (quarter in a year) According to the formula, when interest is compound quarterly: 
Putting the values in the formula, we get: 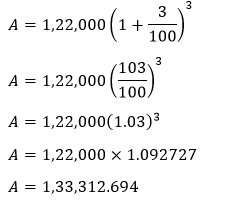
Hence, after 9 months she will get Rs. 1,33,312.694. Example 5: Find the difference between simple interest and compound interest. If the principal amount is Rs. 70,000, the rate of interest is 4% per annum for 3 years. Solution: Given, principal amount (P)=Rs.70,000 According to the formula: 
Putting the values in the formula, we get: 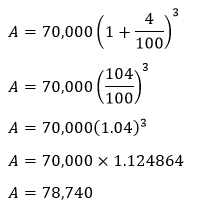
We know that:
Compound Interest (C.I.)=Amount (A)-Principal (P)
Putting the values in the above formula, we get: C.I.=78,740-70,000 Now, we will calculate the simple interest. We know that: 
Putting the values in the above formula, we get: 
Hence, the difference of CI and SI is Rs. 7,900. Example 6: What is the value of a loan of Rs. 3600 after 2 years if the bank imposes 1.5% interest compounded quarterly? Solution: Given, principal amount (P)=Rs.4,100 According to the formula: 
Putting the values in the formula, we get: 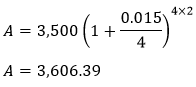
Hence, the value of loans after two years will be Rs. 3,606.39.
Next TopicHow to Find Slope
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





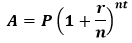
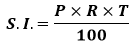
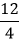 =3% (quarterly)
=3% (quarterly)




