MASON'S GAIN FORMULAThe relation between an input variable and an output variable of a signal flow graph is given by Mason's Gain Formula. For determination of the overall system, the gain is given by: 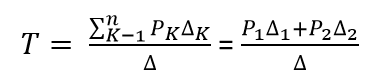
Where,
Pk = forward path gain of the Kth forward path. ∆ = 1 - [Sum of the loop gain of all individual loops] + [Sum of gain products of all possible of two non-touching loops] + [Sum of gain products of all possible three non-touching loops] + ....... ∆k = The value of ∆ for the path of the graph is the part of the graph that is not touching the Kth forward path. 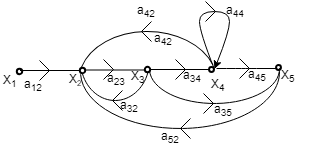
Forward PathFrom the above SFG, there are two forward paths with their path gain as - 
LoopThere are 5 individual loops in the above SFG with their loop gain as - 
Non-Touching LoopsThere are two possible combinations of the non-touching loop with loop gain product as - 
In above SFG, there are no combinations of three non-touching loops, 4 non-touching loops and so on. Where, 
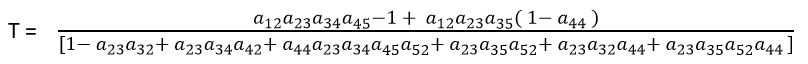
ExampleDraw the Signal Flow Diagram and determine C/R for the block diagram shown in the figure. 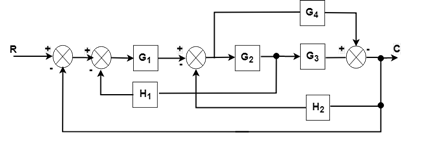
The signal flow graph of the above diagram is drawn below 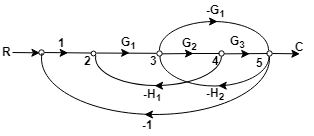
The gain of the forward paths P1 = G1G2G3 ∆1 = 1 P2 = -G1G4 ∆2 = 1 Individual loops L1 = - G1G2H1 L2 = -G2G3H2 L3 = -G1G2G3 L4 = G1G4 L5 = G4H2 Non touching Loops = 0 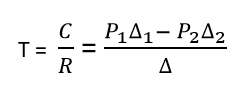
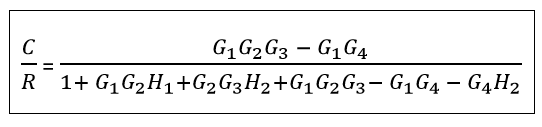
Next TopicExamples with Explanation
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










