State Space ModelThe process by which the state of a system is determined is called state variable analysis. Advantages of State Space Techniques
State Space representation of electrical system:Consider an RLC network, At time t = 0 Current = iL(0) Capacitor Voltage = Vc(0) Thus, the state of the network at time t=0 is specified by the inductor current and capacitor voltage. Therefore iL(0) and Vc(0) is called the initial state of the network and the pair iL(t), Vc(t) is called the state of the network at 't'. The variable iL and vc are called the state variables of the network. 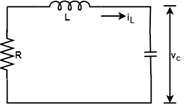
Apply KVL 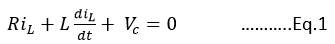
Also, 
From eq.1 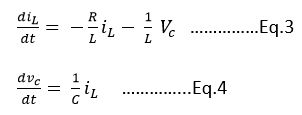
This type of equation is called State equation. And the variables present in this equation are called state variables. Eq. 3 and Eq. 4 can be written in matrix form as 
The general form of state equation is Y = n- dimensional output vector U = r-dimensional control vector or input vector A = n × n system matrix B = n × r control matrix C = n × n output matrix When there is no direct connection between input and output in that case D u(t) is not taken. 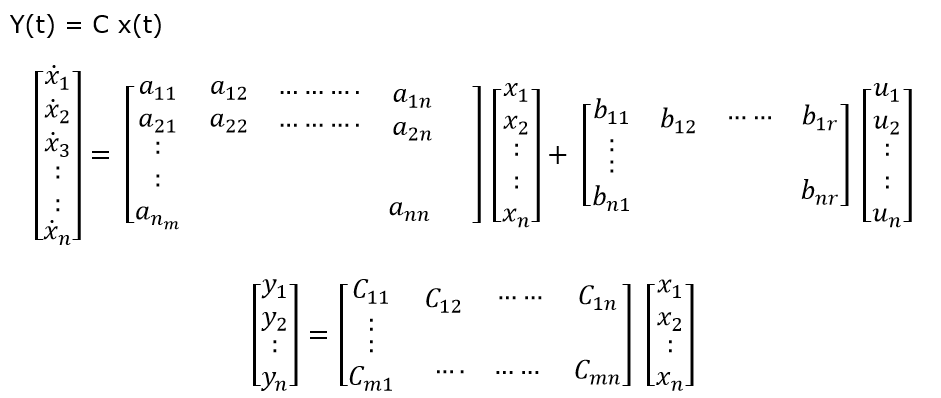
State Space Representation of nth order differential Equation For the nth order differential equation Example 1A system is described by the differential equation 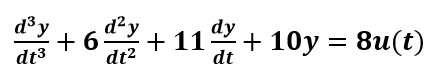
Where y is the output and u is the input to the system. Obtain the state space representation of the system. Solution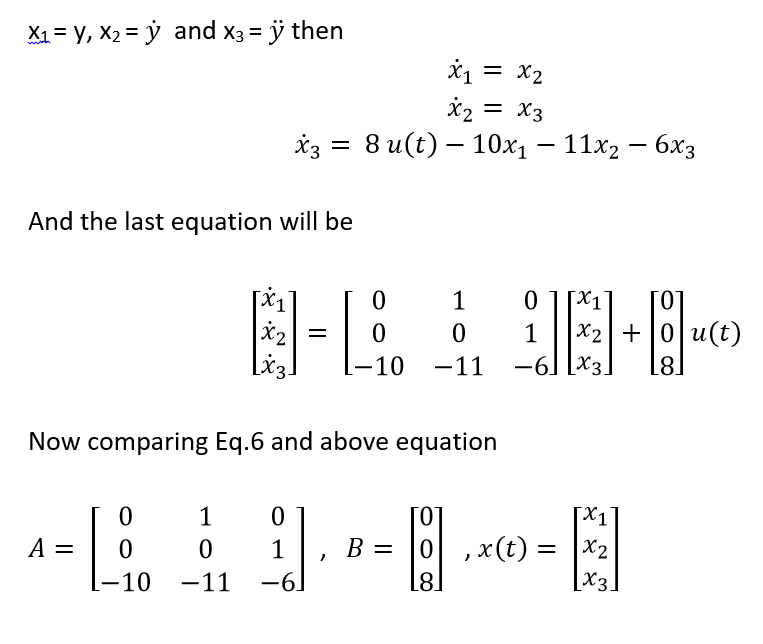
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










