Transfer FunctionThe transfer function of a system is defined as the ratio of Laplace transform of output to the Laplace transform of input where all the initial conditions are zero. 
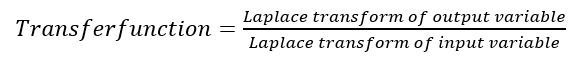

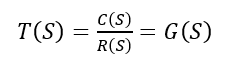
Where, Steps to obtain transfer function -Step-1 Write the differential equation. Step-2 Find out Laplace transform of the equation assuming 'zero' as an initial condition. Step-3 Take the ratio of output to input. Step-4 Write down the equation of G(S) as follows - 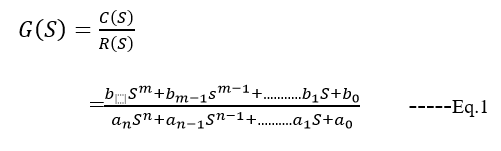
Here, a and b are constant, and S is a complex variable Characteristic equation of a transfer function -Here, the characteristic equation of a linear system can be obtained by equating the denominator to the polynomial of a transfer function is zero. Thus the characteristic equation of the transfer function of Eq.1 will be: an sn+a(n-1) s(n-1)+.........+a1 s+a0=0 Poles and Zeros of a transfer function -Consider the equation 1, the numerator and denominator can be factored in m and n terms respectively: 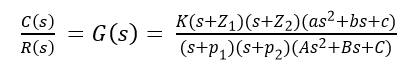
Where,
PolesPoles are the frequencies of the transfer function for which the value of the transfer function becomes zero. ZerosZeros are the frequencies of the transfer function for which the value of the transfer function becomes zero. We will apply Sridharacharya method to find the roots of poles and zeros - 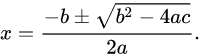
If any poles or zeros coincide then such poles and zeros are called multiple poles or multiple zeros. If the poles and zeros do not coincide then such poles and zeros are called simple poles or simple zeros. For example-Find the transfer function of the following function 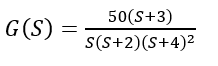
The zeros of the function are S = -3 and the poles of the function are S = 0, S = -2, and multiple poles at S = -4 i.e. the pole of order 2 at S = -4. The two cases that arise when we consider the whole 'S' plane is:1. If the no. of zeros are less than no. of poles, i.e., Z<P then the value of transfer function becomes zero for S?? and the order of such zeros is P-Z. 2. If the no. of poles are less than no. of zeros P<Z then the value of transfer function becomes infinity for S??, and the order of such poles is Z-P. The symbols that are used to locate poles and zeros on S-plane are ?X? and ?O.? The pole is represented by ?X? and zero is represented by 'O.' The pole-zero plot of the above example is as follows - 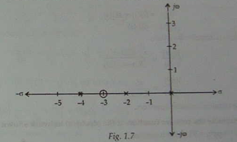
Example -1Find the transfer function of the given network. 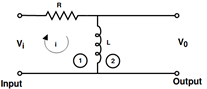
Solution: Step 1 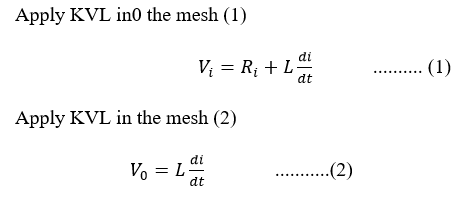

Step 2: By taking the Laplace transform of eq (1) and eq (2) and assuming all initial condition to be zero. 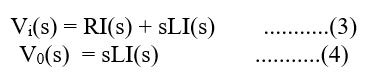
Step 3: Calculation of transfer function 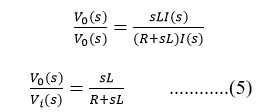
Eq (5) is the transfer function Example- 2Find the transfer function of the following diagram. 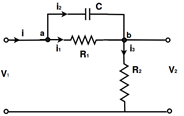
Solution -Step 1:Apply KCL at node 'a.' 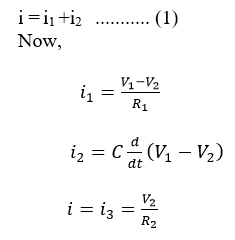
Now putting all the values in eq (1) 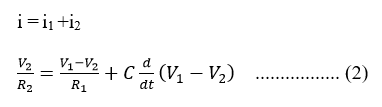
Taking Laplace transform of equation (2) 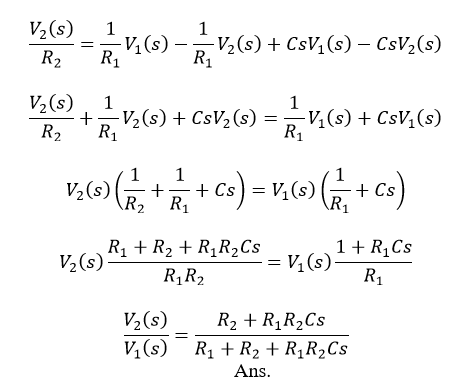
Next TopicBlock diagram in Control Systems
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





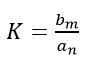 is known as the gain factor and's' is the complex frequency.
is known as the gain factor and's' is the complex frequency.




