Introduction of Convolutional Neural Network in TensorFlow

Convolutional Neural Network is one of the technique to do image classification and image recognition in neural networks. It is designed to process the data by multiple layers of arrays. This type of neural network is used in applications like image recognition or face recognition. The primary difference between CNN and other neural network is that CNN takes input as a two-dimensional array. And it operates directly on the images rather than focusing on feature extraction which other neural networks do.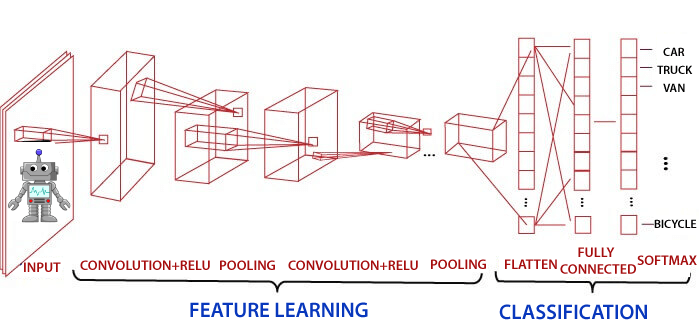

The dominant approach of CNN includes the solution for problems of recognition. Some companies like Google and Facebook have invested in the field research and development concerning recognition projects to get activities done with higher speed.

Scene labeling, object detection, and face recognition, etc. are some of the areas where Convolutional Neural Network works.

Convolutional Neural Network (CNN or ConvNet) is a type of feed-forward artificial network where the connectivity pattern between its neurons is inspired by the organization of the animal visual cortex.

The visual cortex has a small region of cells that are sensitive to specific regions of the visual field. Some individual neuronal cells in our brain respond in the presence of edges of a certain orientation.

Origin of Convolutional Neural Networks

The intelligence of neural networks is unnatural. While the artificial neural network is researched as early in the 1960s by Rosenblatt, it was only in late 2000s when deep learning using neural networks took off. The key enabler was the scale of computation power and datasets with Google developing research into deep learning. In July 2012, researchers at Google disclosed an advanced neural network to a series of unlabeled, static images sliced from YouTube videos.

For example,

Consider this image of Nature, upon first glance; we will see a lot of buildings and colors.

How Does a Computer read an image?

The image is broken into 3 color-channels which is Red, Green, and Blue. Each of these color channels is mapped to the image's pixel.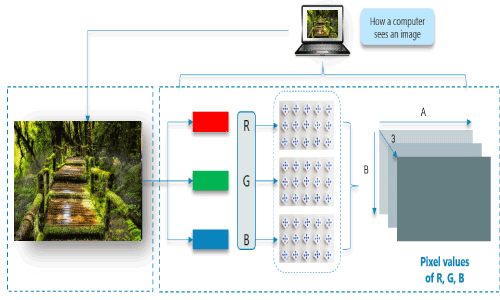

Some neurons fires when exposed to vertices edges and some when shown horizontal or diagonal edges. CNN utilizes spatial correlations which exist with the input data. Each concurrent layer of the neural network connects some input neurons. This region is called a local receptive field. The local receptive field focuses on hidden neurons.

The hidden neuron processes the input data inside the mentioned field, not realizing the changes outside the specific boundary.

Convolutional Neural Networks have the following 4 layers:

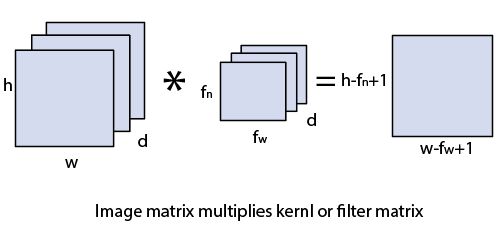
• Convolutional
• ReLU Layer
• Pooling
• Fully Connected

Convolutional layer

Convolution layer is the first layer to derive features from the input image. The convolutional layer conserves the relationship between pixels by learning image features using a small square of input data. It is the mathematical operation which takes two inputs such as image matrix and kernel or any filter.

• The dimension of image matrix is h×w×d.
• The dimension of any filter is f_h×f_w×d.
• The dimension of output is (h-f_h+1)×(w-f_w+1)×1.

ReLU Layer

Rectified Linear unit(ReLU) transform functions only activates a node if the input is above a certain quantity. While the data is below zero, the output is zero, but when the input rises above a certain threshold. It has a linear relationship with the dependent variable.

In this layer, we remove every negative value from the filtered images and replaces them with zeros.

It is happening to avoid the values from adding up to zero.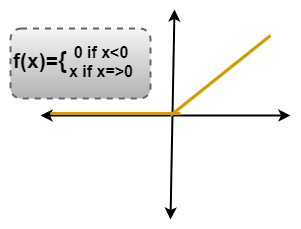

Pooling Layer

Pooling layer plays a vital role in pre-processing of any image. Pooling layer reduces the number of the parameter when the image is too large. Pooling is "downscaling" of the image achieved from previous layers. It can be compared to shrink an image to reduce the image's density. Spatial pooling is also called downsampling and subsampling, which reduce the dimensionality of each map but remains essential information. These are the following types of spatial pooling.

We do this by implementing the following 4 steps:

• Pick a window size (usually 2 or 3)
• Pick a stride (usually 2)
• Walk your window across your filtered images
• From each window, take the maximum value

Max Pooling

Max pooling is a sample-based discretization process. The main objective of max-pooling is to downscale an input representation, reducing its dimension and allowing for the assumption to be made about feature contained in the sub-region binned.

Max pooling is complete by applying a max filter in non-overlapping sub-regions of initial representation.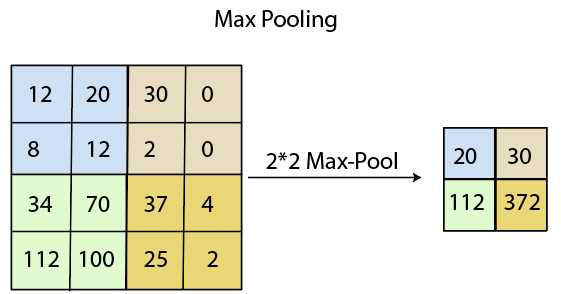

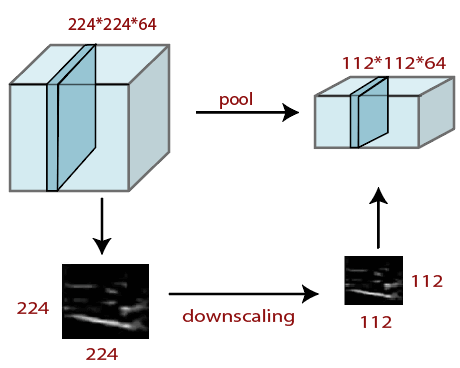
Average Pooling

Down-scaling will perform by average pooling by dividing the input into rectangular pooling regions and computing the average values of each area.

Syntax

Sum Pooling

The sub-region for sum pooling and mean pooling are set the same as for max-pooling but instead of using the max function we use sum or mean.

In this layer we shrink the image stack into a smaller size steps;

1. Pick a window size (usually 2 or 3)
2. Pick a stride (usually 2)
3. Walk our window across our filtered images.
4. From each window, take the maximum value.

Performing pooling with a window size two and stride 2.

Fully Connected (Dense) Layer

The fully connected layer (dense layer) is a layer where the input from other layers will be depressed into the vector. It will transform the output into any desired number of classes into the network.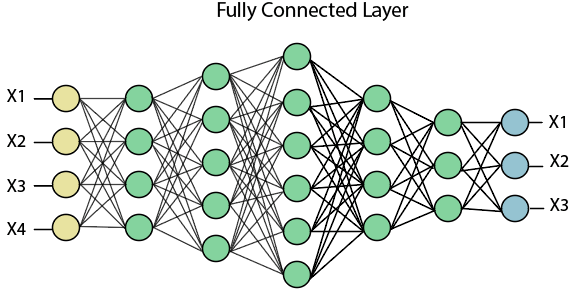

In the above diagram, the map matrix is converted into the vector such as x1, x2, x3... xn with the help of a fully connected layer. We will combine features to create any model and apply activation function like as softmax or sigmoid to classify the outputs as a car, dog, truck, etc.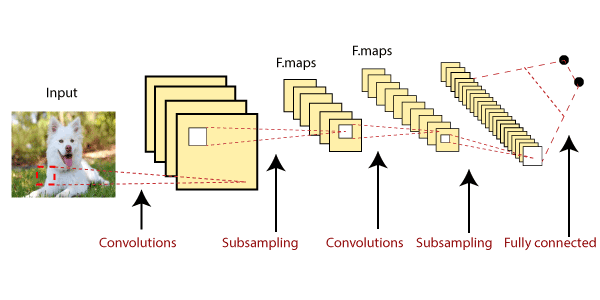

This is the final where the actual classification happens.