Crystal OscillatorThe crystal oscillator is a quartz crystal used as a frequency selective element. The quartz crystal is also known as piezoelectric crystal. Hence the oscillator circuit containing piezoelectric crystal is called a crystal oscillator. It has two electrodes that supply signals to the crystal. Crystal oscillators have high-frequency stability and a high-Quality factor compared to RC and LC tuned circuit oscillators. It is considered one of the highly stable oscillators suitable for high-frequency applications. What is a crystal?A crystal is a solid substance with atoms and molecules tightly packed in a three-dimensional shape. Most solid objects have their resonant and frequency of vibrations. The object made of the elastic material with the resonant and frequency of vibrations is crystal. The resonant frequency also depends on the speed of the sound in a solid object, such as steel. Steel is a metal alloy that has a high speed of sound. The advantages of using quartz crystals are as follows:
The circuit of a crystal oscillator is shown below: 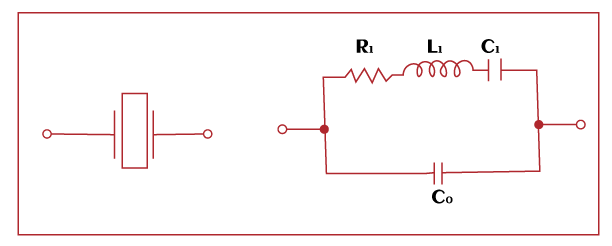
The quartz crystal is attached in parallel with the resonant circuit of the oscillator. The resonant circuit includes a resistor, capacitor, and an inductor connected in series. Co is the static capacitance associated with the quartz crystal. PrincipleThe applied voltage across the crystal helps it to vibrate at its natural frequency. The vibrations produced by the piezoelectric crystal get converted into oscillations. WorkingThe input signal is applied to crystal oscillator circuit. It consists of a crystal and the resonance circuit, as shown above. The signal first passes through the electrodes of the quartz crystal. It changes its shape due to the applied voltage. When the voltage is removed, the crystal returns to its original shape. The crystal generates a small voltage before returning to its original position. The piezoelectric crystal uses the electrical signal to produce vibrations. It means that the crystal converts electrical energy into mechanical energy. The vibrations get converted into oscillations of constant frequency. The other terminal converts the mechanical energy back to electrical energy. The produced oscillations of constant frequency act like an RLC circuit. Once a crystal is adjusted to a specific frequency and other environmental factors, it starts maintaining a high frequency or high-Quality factor. 
The crystal oscillators cover frequencies below 1000 Hz and above 200M Hz. Static capacitanceCo is the static capacitance connected in parallel with the RLC combination, as shown above. The resistor, inductor, and capacitor are connected in series. The impedance can be represented as: Z(s) = (1/sC1 + sL1 + R1) Another capacitor Co was connected in parallel. Z(s) = (1/sC1 + sL1 + R1) || 1/sCO 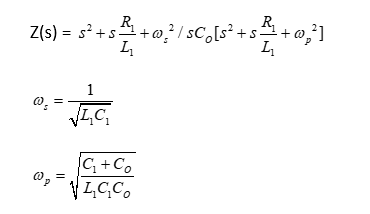
Putting the value of ?s in the above equation, we get: 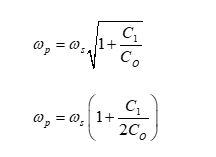
Where, ?s is the series resonant angular frequency ?p in series resonant angular frequency History
Stability analysis of Crystal oscillatorsThe frequency stability of a crystal is based on the Quality-factor. The oscillator's Q factor is inversely related to its frequency. The factor that influences the Q-factor includes temperature, mechanical stress, aging, and radiation damage. Let's discuss these factors in detail. TemperatureThe temperature variations can directly influence the operating frequency of the oscillator. The crystal ovens are used in such cases to stabilize the temperature. The crystal oven is a temperature-controlled chamber that helps the crystal to maintain a constant temperature to avoid any fluctuations in the frequency. Different types of compensators are used along with the crystal ovens, such as microcontroller compensators. Mechanical StressThe electrodes, crystal, and bonding materials can generate stress in oscillators. It occurs due to the expansion or contraction of the bonding material, defects or impurities in the crystal, or by the effect of gravity on the crystal. Other types of mechanical stress are vibrations, change in atmospheric pressure, and noise. The careful design and transducers in the oscillator can help overcome mechanical stress. AgingThe gradual deformation of the crystal with time is known as aging. It results in the frequency changes in the oscillator. The differences in the packaging of the electrodes, diffusion of impurities, etc., are the reasons that cause aging in the oscillator. Various metals are used to prevent aging, such as gold, silver, and aluminum. The gold handles strong mechanical shocks but does not form oxides. Silver and aluminum are used for making electrodes and easily form oxides. Radiation DamageThe crystals are sensitive to the incident radiations. It can be reduced by heating the crystal at high temperature of about 400 degrees Celsius in an electric field in a hydrogen free environment. Such crystal responds slowly to the incident radiations. Frequency AccuracyThe frequency accuracy of the crystal oscillator lies between the range 10-6 and 10-7. The range includes all other environmental factors, such as temperature changes and aging. The stabilities of the precision quartz oscillator lie between the range 10-10 and 10-12. The precision quartz oscillators are protected from any external environmental disturbances. It also works at a constant temperature with very few frequency fluctuations and long-term accuracy. AdvantagesThe advantages of crystal oscillator are as follows:
DisadvantagesThe disadvantages of crystal oscillator are as follows:
Numerical ExamplesExample: In the equivalent circuit of the crystal oscillator, L = 2H, C1 = 0.04p Farads, Co =10p Farads, and R = 2000 Ohms. Find the series and parallel resonant angular frequency. Solution: Given: L = 2H C1 = 0.04p Farads = 0.04 x 10-12 F = 4 x 10-14 Farads Co =10p Farads = 10 x 10-12 F =10-11 Farads R = 2000 Ohms Fs = Series resonant angular frequency 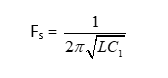
Fs = 1/ 2 x 3.14 x (1 x 4 x 10-14)1/2 Fs = 1/ 2 x 3.14 x 2 x 10-7 Fs = 1/ 12.56 x 10-7 Fs = 0.796 x 106 Hz Fs = 0.796M Hz Fs =796k Hz 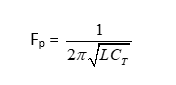
CT = 0.04 x 10 / 0.04 + 10 CT = 0.4/ 10.04 CT = 0.0398 pF Fp = 1/ 2 x 3.14 x (1 x 3.98 x 10-14)1/2 Fp = 1/ 2 x 3.14 x 1.99 x 10-7 Fp = 1/ 12.52 x 10-7 Fp = 0.798 x 106 Hz Fp =0.798M Hz Fp =798k Hz Thus, if the oscillator is a crystal oscillator, the frequency of oscillations will lie between796k Hz and 798k Hz.
Next TopicLC Oscillators
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










