Density formula

The density of a substance is defined as mass per unit volume. Mathematically, we can define density as mass divided by volume. The density formula can be represented as: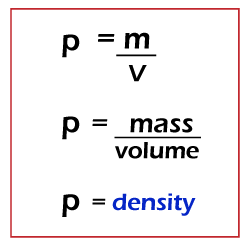

The symbol of density is rho. It is also be represented by D. Density defines how tightly the molecules of the substance are packed together.

M is the Mass that is measured in Kilograms (Kg) or grams (g). Here, 1kg = 1000g.

V is the volume that is measured in meter cube (m^3) or centimeter cube (cm^3).

Thus, the unit of density can be kilograms per meter cube (Kg/m^3) or grams per centimeter cube (g/cm^3).

The density formula was discovered by Archimedes. He was an engineer, inventor, mathematician, physicist, and astronomer (studying celestial objects). Inspired by the inventions of the Archimedes on density, Galilio Galilei invented a hydrostatic balance that could measure the metal weights in air and water.

Different materials exhibit different densities. For example, osmium is the densest element known under standard conditions.

Here, we will discuss examples of density, measurement of density, measurement, units of density, Numerical examples, and MCQs based on the density formula.

Examples of density

Here, we will discuss the least and most dense materials. Dense materials are hard materials. For example, a material with stuff or strong packaging in the space is denser than the loose packing material.

The denser materials are categorized as uranium, god, tungsten, platinum, etc. The atoms of these substances are tightly packed around the nucleus. Such materials are also heavy.

The materials with low density are categorized as grapheme, hydrogen, etc. These materials have the lowest atomic weight and thus the least density.

Let's discuss the density of solid, liquids, and gas.

We know that the atoms of the solid are packed more tightly than the liquids and gas. Hence, solids have rigid structure. The atoms of liquids are loosely bound and can be transferred into any shape. The atoms of the gas are very loosely packed and can move quickly in space. It predicts that the gases have the least density and the solids have the maximum density. The liquids generally have medium-density that lies between the solids and gases.

Let's consider the densities of few substances. It is shown in the below table.

The above table clearly depicts the densities of various substances, where solids (aluminum and diamond) have high densities and gases (hydrogen and helium) have lowest densities.

Measurement of density

We have discussed the density formula, and the density of materials. But, do we know that how the density is measured? Let's discuss this in detail.

The main method to determine the density of a substance is to divide the mass by volume, as discussed above. A weighing scale can measure the mass of a substance in grams or kilograms. Similarly, volume can be calculated by performing mathematical calculations based on the formula.

But, how can we measure the mass of the gas? We can use the concept of molar mass to measure the gas density.

Another method to determine the density of liquids is the device called a hydrometer. It can measure some characteristics of liquids, such as special gravity and density. Thought, a convenient method of measuring density is the weighing scale that has high accuracy as compared to other methods.

Units of density

Density = Mass/volume

The unit of mass is kg and the unit of volume in meter cube.

Thus, the unit of density = kilograms/meter cube

= kg/m^3

= kilograms per meter cube.

Other units

The S.I unit of density is kilograms per meter cube, but we can also express it with other units. S.I or the International System of Units is the only official system of measurement whose units are accepted worldwide. Other units of density are as follows:

• Kilograms per liter (Kg/L).
• One gram per centimeter cube (1 gm / cm^3).
• Gram per Milliliter (gm / mL).
• Kilogram per cubic decimeter (Kg / dm^3)
• Metric ton per cubic meter (t/m^3).
• Lb/ft^3.

Dimensional formula of density

As discussed, density is defined as the ratio of mass and volume.

Density = Mass/volume

The dimensional unit of mass is M, while of volume is L^3.

Density = M/L^3

= ML^-3

Let's discuss numerical examples and Multiple Choice Questions related to density formula for better understanding.

Numerical Examples

Consider the following numerical examples.

Example 1: A substance has amass of 200g and the volume of 5.5 m^3. What is the density of the substance?

Solution: The given parameters are:

Mass = 200g = 200/1000 = 0/2kg

Volume = 5.5 m^3

Density =mass/volume

Density = 0.2/5.5

= 0.36 kg/m^3.

Thus, the density of the substance is 0.36 kg/m^3.

Example 2: The mass of a cube is 500g and the edge length of the cube is 10cm. What is the density of the cube?

Solution: We can calculate the density either in g/cm^3 or kg/m^3. We can also compute the direct formula to convert g/cm^3 to kg/m^3. Let's find the value of density in both units.

Method 1:

The given parameters are:

Mass = 500 g

Edge length = 10cm.

Volume of a cube = (edge length)^3 = 10 x 10 x 10 = 1000cm^3

Density of the cube = mass/volume

=500/1000

= 0.5 g/cm^3.

Method 2:

The given parameters are:

Mass = 500 g = 500/1000 =0.5kg (1000g = 1kg)

Edge length = 10cm = 10/100 = 0.1m (1m = 100cm)

Volume of a cube = (edge length)^3 = 0.1 x 0.1 x 0.1 = 0.001 m^3

Density of the cube = mass/volume

= 0.5 / 0.001

= 500 kg/m^3

We can also compute the direct formula to convert g/cm^3 into kg/m^3.

Method 3:

It is given by:

1g/cm^3 = 1000kg/m^3

So,

0.5 g/cm^3 = 1000 x 0.5 = 500 kg/m^3

Example 3: A solid ball has a mass of 100 grams and a radius of 2cm. What is the density of the solid ball?

Solution: The given parameters are as follows:

Mass = 100g

Radius = 2cm

The shape of a ball is similar to that of sphere. So, the volume of a sphere is given by: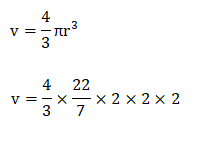

So, volume = 33.52 cm^3

Density = mass/ volume

= 100 / 33.52

= 2.98 g/cm^3

Thus, the density of the solid ball is 2.98 g/cm^3.

Example 4: Diamond has a density of 3500 kg/m^3 and the volume of 0.01 m^3. What is the mass of the substance?

Solution: The given parameters are as follows:

Density: 3500 kg/m^3

Volume = 0.01 m^3

We know that the density = mass/ volume

So, mass = density x volume

Mass = 3500 x 0.01

= 35 kg

Thus, the mass of the substance is 35 Kilograms.

MCQs based on density formula

Let's discuss some Multiple Choice Questions on density formula.

1) The unit of density is:

1. Kg/cm^3
2. g/m^2
3. kg/m^3
4. kg/m^2

2) Densities of which substances do not change with pressure.

1. Solids, gases
2. Solids, liquids
3. Liquids, gases
4. All of the above

3) The density of air in kg/m^3 is:

1. 2.0
2. 1.63
3. 1.2
4. 2.5

4) The density of a substance is 3.45 g/cm^3. What is the density in kg/m^3?

1. 3450 kg/m^3
2. 345 kg/m^3
3. 34.5 kg/m^3
4. 0.0345 kg/m^3

5) Mass divided by volume is called:

1. Force
2. Density
3. Mole fraction
4. None of the above