Detect cycle in a directed graphIn a directed graph, we will check whether the graph contains cycle or not. A directed graph is a set of vertices or nodes connected by edges, and each edge is associated with some direction. Consider the below directed graph to detect the cycle. 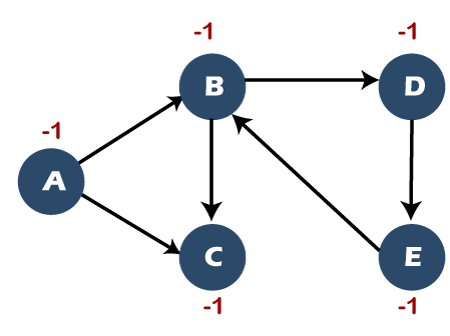
Now, we will use the DFS technique to detect cycles in a directed graph. As we are using the DFS technique, so we will use the stack data structure for the implementation. Here, we will use the flag variable that contains three values, i.e., 0, 1, and -1. Here, 0 means that the node is visited and available in the stack, -1 means that the node is unvisited, and 1 means that the node is visited and has been popped out from the stack. Initially, all the vertices are marked with -1 as they all are not visited. Step 1: First, we will visit vertex A and will be marked as 0. Since node A has been visited so it will be marked as 0, and node A is pushed into the stack shown as below: 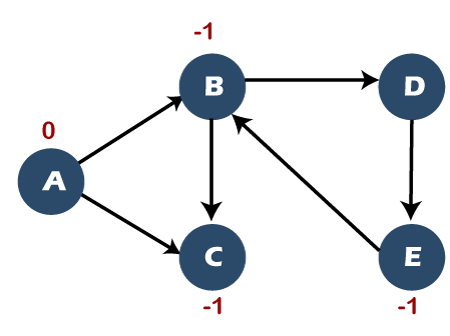

The visited set contains the node A shown as below: Visited set: A The parent map table is given below: 
Since node A has been visited, A comes under the vertex column and the parent column is left blank as node A is a source vertex. Step 2: The next vertex is B. Now, we will visit vertex B and will be marked as 0. Since the node B has been visited so it will be marked as 0, and node B is pushed into the stack shown as below: 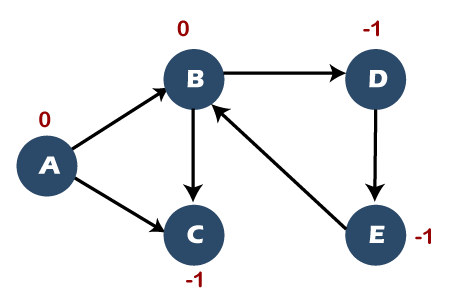
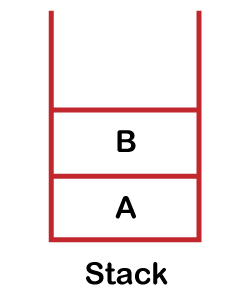
The visited node contains the nodes A and B shown as below: Visited set: A, B The parent map table is shown below: 
Since node B has been visited, so B comes under the vertex column, and A comes under the parent column as B comes from node A. Step 3: The adjacent vertices of B are C and D means we can either visit C or D. Suppose we visit vertex C, so vertex C will be marked as 0 and node C is pushed into the stack shown as below: 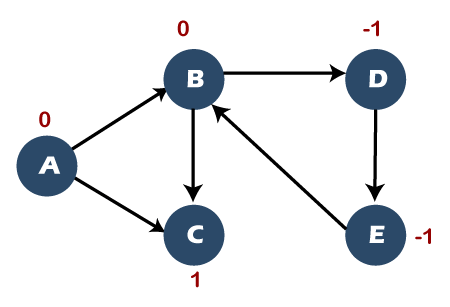
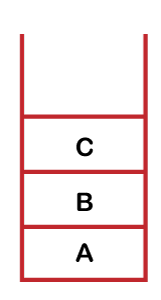
Now, the visited set contains the nodes A, B, and C shown as below: Visited set: A, B, C The parent map table is shown below: 
Since node C has been visited, so C comes under the vertex column, and B comes under the parent column. Step 4: There are no further vertices to be visited from C, so we will perform backtracking. In order to perform backtracking, we will pop the node. First, we will pop node C from the stack. Since node C has been popped out, so we will mark the node C as 1 shown as below: 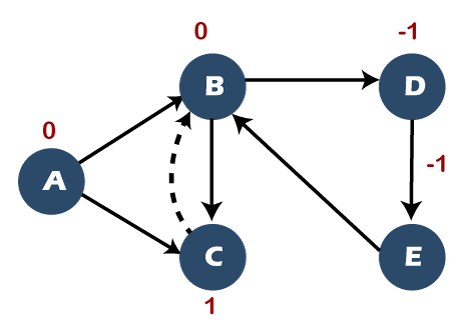
The next topmost node in the stack is B, so we will backtrack to the vertex B shown as below: Step 5: Now, we will see 'is there any adjacent vertex left to be visited'. We can observe in the above graph that the vertex D is left unvisited. So, now we will move from the vertex B to the vertex D. The flag value of vertex D is now changed to 0, and the vertex D is pushed into the stack shown as below: 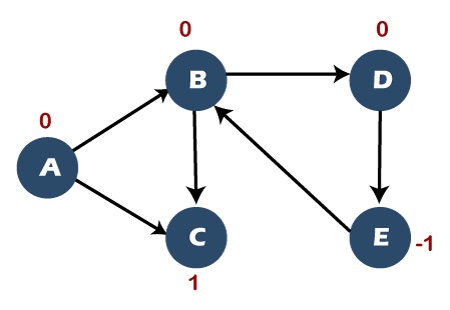
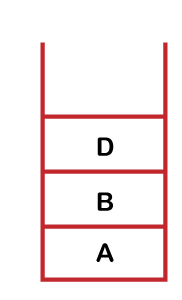
Now the visited set contains the nodes A, B, C, D The parent map table is shown below: 
Since node D has been visited, it comes under the vertex column, and the node D has arrived from vertex B, so vertex B comes under the parent column. Step 6: The adjacent vertex of node D is node E which is left unvisited. Now we will visit the vertex E and will mark its flag value as 0. The node E is pushed into the stack shown as below: 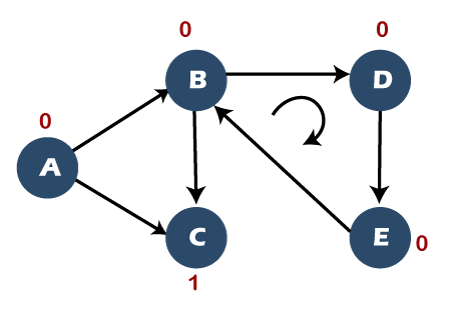
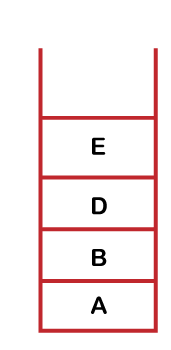
Now, the visited set contains the nodes A, B, C, D, E. The parent map table is shown below: 
Since node E has been visited, it comes under the vertex column, and node E has arrived from the vertex D, so D comes under the parent column. Condition There is one condition that determines whether the graph contains a cycle or not. If the adjacent vertex of any vertex is having a 0 flag value means that the graph contains a cycle. In the above graph, the adjacent vertex of E is B, and its flag value is 0; therefore, the graph contains a cycle. Now we will determine the nodes that create a cycle in a graph. The adjacent vertex of E is B; E->B The parent of E is D so; D->E->B The parent of D is B so, B->D->E->B (creates a cycle)
Next TopicOptimal Binary Search Tree
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










