Difference between Scalar Quantity and Vector Quantity

According to the classification, a physical quantity is a measurable and quantifiable physical property that includes unique information. Every physical explanation can be stated using several physical quantities, each with its significance and importance. Physical quantities are categorized into two types based on their dependency on the direction; scalars and vectors. Both of these quantities are used to represent an object's motion.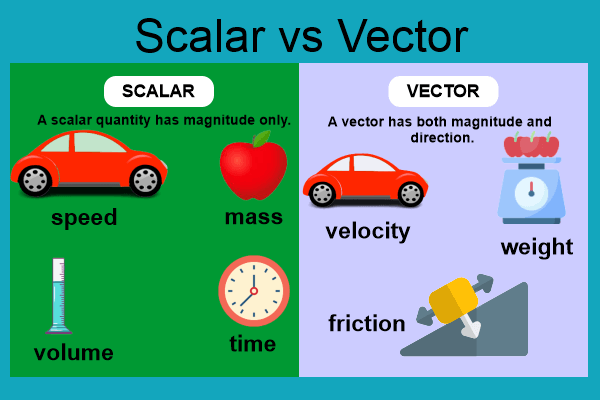

Scalar Quantity

A scalar quantity has no direction and only magnitude. Scalars have no direction such as length, mass, duration, speed, etc. Scalars have no application in direction, so their value is the same in all directions. As a result, each scalar has a single dimension.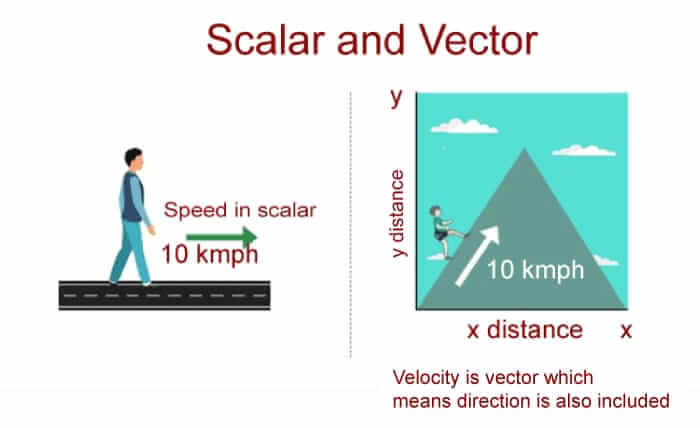

Any change in a scalar quantity only represents a change in magnitude because it has no relation with direction. Scalar values can be combined according to standard algebraic rules, allowing them to be added, subtracted, or multiplied in the same manner as numbers. Scalar quantities will be handled with the same measuring unit. The multiplication of 2 scalar quantities will produce the dot product.

Scalar Relation with Mathematics

In mathematics, a scalar is a component of a mathematical field that is used to describe a vector space, just as it is in physics. An element of a field that is utilised to define a vector space is referred to as a scalar. The procedure of scalar multiplication, which is defined in association with vector space, allows a vector to be multiplied by a scalar in the defined method to produce another vector. In linear algebra, real numbers are usually the field elements which are referred to be scalars and relate to vectors in the vector space. Any field can be used to define a vector space in place of real numbers (such as complex numbers). Scalars of that vector space will then be components of the corresponding field.

Physiologically in the electric field strength is also a scalar because the inner product is independent of any vector space basis. A change in the vector space basis does not affect an object's mass, making it a physical scalar that can be characterised as an element in the real number field.

Examples of Scalar Quantities

• Area

There is just magnitude when calculating the surface area of land or other two-dimensional objects. When measuring a three-dimensional object, you can attach a direction to it because you are measuring it from several angles. However, when the measurement is straightforward and two-dimensional so the area is scalar.

• Density

By dividing a unit's mass by its volume, you may get its density. It is a scalar quantity because the calculation only requires two points. An object's density is independent of direction.

• Distance

When you measure distance, the amount of space you have covered is given. The scalar quantity of distance solely describes how much distance was covered it does not include displacement and speed.

• Energy

As the result of the product of two other variables (displacement and force, in this case) energy is a scalar quantity. Without taking direction into consideration, it describes the size of energy consumption.

• Speed

The distinction between velocity and speed might be difficult to explain. However, as direction is irrelevant for measuring speed, understanding that speed is indeed a scalar variable will be useful.

Vector Quantity

A vector quantity has both a magnitude and a direction. When defining or stating a vector quantity, the direction of action with its value or magnitude will also be specified. Vectors can be displacement, weight, force, and velocity.

In vector, magnitude signifies the quantity's size, and its absolute value and direction represent the side, such as east, west, north, south, and so on Vector quantities can be expressed in terms of one or two- or three-dimensional parameters. Any change in the vector quantity implies either a change in magnitude, direction or both. You can resolve a vector using the sine or cosine of adjacent angles (vector resolution). The triangle law is used to add a vector quantity. The vector product between two quantities will be the cross product.

Vector Relation with Mathematics

Vectors were first used in geometry and physics to represent quantities with a magnitude and a direction, including displacements, forces, and velocity (typically in mechanics). In mathematics, Vectors are defined as objects that have both magnitude and direction. The vector's size is determined by its magnitude. It is represented in line with an arrow, where the line's length represents the vector's magnitude, and the arrow will represent the direction. In some contexts, the term vector also refers to tuples, finite segments of a fixed length of numbers. It is also referred to as a Euclidean vector, Geometric vector, Spatial vector, or simply "vector."

Examples of Vector Quantity

• Acceleration

Acceleration is the rate at which the object's velocity will be changed. It considers both time and direction, causing it to be a vector quantity.

• Temperature

The temperature of the medium is measured as a scalar quantity. However, measuring the rise or fall in the temperature of the medium is a vector quantity since it has both magnitude and direction.

• Polarization

Polarization signifies that two units move from one side to another which is magnitude (how far or how much) as well as the direction (away from each other) are important factors in measuring polarisation implying that it is a vector quantity.

• Momentum

Momentum signifies the movement of an object. You can calculate it if you know how quickly and in which direction an object is going because it shows the product of mass and velocity (the magnitude).

• Weight

An object's weight is calculated by multiplying its mass by the acceleration of gravity acting on it. Weight has a magnitude as well as a direction (down) because it includes the force of gravity.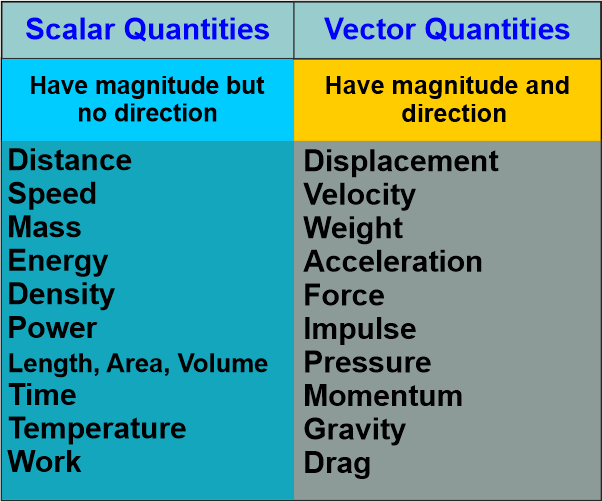

Similarities between Scalar and Vector Quantity

• Scalar and vector quantities both reflect distinct physical quantities, and both have a finite range of magnitude.
• Both scalar and vector variables are quantifiable and measurable (can be measured using an appropriate instrument).

Difference between Scalar and Vector Quantity

Now, let us talk about how scalar and vector quantities differ from one another. According to the concept, a physical quantity is an identifiable physical property that can be measured and quantified. Each physical quantity expresses a unique significance and value in that context and can be used to describe any scientific explanation. Physical values can be categorized as either scalar or vector depending on how dependent they are on the direction. An object's motion is represented by both of these numbers.

Conclusion

In conclusion, scalar quantity gives you a sense of the quantity of an object. However, vector quantity provides information on an item's amount and direction. When comparing two scalar quantities, you need to consider magnitude. On the other hand, when we compare two vector quantities, it is necessary to consider both magnitudes as well as directions. This makes dealing with vector quantities more challenging than dealing with scalar quantities. A scalar quantity can be divided into another scalar. However, when dealing with a vector quantity, this is not possible. As a result, the primary distinction between scalar and vector quantity is direction. In other words, vectors have direction but scalars do not.