Difference between Simple Interest and Compound Interest

Interest

The amount or percentage that the borrower must pay as an additional fee to the lender is known as interest. We can sum up interest as the cost of borrowing money in one sentence. The entire world economy is dependent on the value of money. A Dollar today cannot be a Dollar tomorrow; this means that the value of a Dollar is not always constant it changes with time.

Similar to how money deposited in a bank or building society account frequently earns interest, a borrower typically has to pay interest on money borrowed. The rate of interest is usually (but not always) quoted as a rate per cent per year. At the time of writing a typical rate is 1.5% per annum for money deposited and 1%-2% per annum for money borrowed. Up-to-date rates are available from finance organizations.

Some terminologies related to the term interest:

A creditor is a person who lends money, whereas a debtor is a person who borrows money.

Capital or principal money is the sum of money that is initially borrowed.

The period for which money is deposited or borrowed is called Time.

The extra money that will be paid or received for the use of the principal after a certain period is called the Total interest on the capital.

The sum of the principal and the interest at the end of any time is called the Amount. So, Amount = Principal + Total Interest. The rate of interest, which is always expressed in percentage terms, is the rate at which interest is calculated.

There are two basic ways of calculating the amount of interest paid on money deposited:

Simple Interest and Compound Interest

1. Simple Interest:

It is determined using a basic amount borrowed for the entire time period at a specific interest rate. The principle for the full loan time is the amount borrowed. We may compute the interest due on a specific amount lent over time using a simple interest formula.

Simple interest is calculated by keeping the principal amount constant, which streamlines the calculation and reduces the amount of interest owed by the borrower.

The total amount is the sum of the principal and interest payments made by the borrower to the lender.

The formula to calculate Simple Interest is given below:

In the above formula, the terminologies used can be defined as:

• Principal (P): It is the amount borrowed. The basis for interest payments is the amount borrowed. The interest rate will increase in direct proportion to the amount borrowed. Unlike the compound interest formula, the principal amount will remain the same until the borrowed amount is repaid.
• Rate(R): It is the interest rate at which money is lent. The interest payable would rise proportionately to the interest rate on the same principal amount. For instance, if someone borrowed Rs. 2,00,000 at a 10% interest rate, they would be required to pay Rs. 20,000 in interest. In contrast, if the interest rate was 20%, he would be required to pay Rs. 40,000 in interest for the same amount
• Time (T): It is the period for which the amount would be borrowed. This can be in terms of days, months, or even years.

Applications of Simple Interest:

It is easy to calculate.

Widely used in real life.

Used for commercial deposits in the Banks.

Used by businesses to provide financial help in purchasing products.

Car Loan:

Due to the fact that auto loans are due monthly, each month the principal component of the loan is reduced while the remaining amount is used to pay the interest charges.

Every month, the amount of interest due falls together with the balance of the loan that is still owed.

A sample example is given below to clarify the concept.

Aman borrowed Rs 2,54,648 from a corporation. He was offered to borrow at a rate of 13.45% for 12 months. Find out the total payable amount.

Given information:

Principal amount = 2,54,648

Rate of Interest = 13.45%

Time period= 12 months

Also,

Simple interest = (Principal x time period x rate of interest)/100

By putting given values in the above formula, we get,

Simple Interest = (2,54,648 x 1 x 13.45 )/100

= 34,250 (approx.)

Therefore, the total payable amount is Principal+ Simple Interest

= 2,54,648 + 34,250

= 2,88,898

2. Compound Interest

In financial transactions, the borrower and the lender frequently agree to a specific amount of interest to be paid to the lender on the basis of a predetermined unit in order to settle an account in time. This can take place yearly, semi-annually, or quarterly, as long as the interest that has accrued on the principal at a certain point in time is added to the principal and the total at the conclusion of one period becomes the principal for the following interval. Thus, it is different from simple interest.

In such cases, the interest for the first interval is added to the principal and this amount becomes the principal for the second interval, and so on. Compound interest for the specified period is the difference between the amount and the borrowed funds.

For the purpose of calculating compound interest, the interest from the prior year or years is/are added to the principal.

The following example will make this distinction obvious:

A sum of Rs.1000 at 10% per annum will have

In this case of compound interest, take note that the interest from prior years is added to the initial sum of 1,000 to determine the final amount of interest to be paid.

With Compound Interest, you work out the interest for the first period, add it to the total, and then calculate the interest for the next period, and so on, like this:

All values in Rupees,

1000 (+10%=100) → 1100 (+10%=110) → 1210 (+10%=121) → 1331 …. and so on...

The formula to calculate Compound Interest is given below: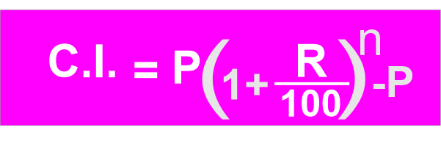

Here,

P is the initial principal amount.

CI is the Compound Interest.

R is the rate of the interest per annum.

and n is the time.

Application of Compound Interest:

• Helpful in Bank transactions.
• Increase in the value of the item.
• Inflation in the profit and the loss.

Some Points about Compound Interest

• Interest is paid on money that has already been used to pay interest. Good for savings and investment.
• Can work against you in paying interest on a loan.
• Compound Interest causes interest and account balances to grow for lenders.

Compound Interest is not necessarily calculated annually, it can be calculated semi-annually, quarterly, monthly, or even daily. Cases are discussed below:

1) Calculation of Semi-annually Compound Interest:

CI = P (1+ r/200)^2t - P

2) Calculation of Quarterly Compound Interest:

CI = P (1+ r/400 )^4t - P

3) Calculation of monthly Compound Interest:

CI = P (1+ r/1200)^12t - P

4) Calculation of Daily Compound Interest:

CI = P (1+ r/36500)^365t - P

Sample Solved Examples to Clear the Concept

If CI is charged on a certain sum for 2 years at 10% per annum the amount becomes Rs. 605. Find the principal?

(a) Rs.550 (b) Rs.450

(c) Rs.480 (d) Rs.500

Solution:

Using the formula, amount = Principal (1 + rate/100)^t

605 = p (1 + 10/100)²

p = 605(100/121) = Rs. 500.

If the difference between the CI and SI on a certain sum of money is Rs. 72 at 12 per cent per annum for 2 years, then find the amount.

(a) Rs.6000 (b) Rs. 5000

(c) Rs.5500 (d) Rs. 6500

Solution:

Let the principal = p

Simple interest = (p x 12 x 2)/100

Compound interest = p [1 + 12/100]² - p

So, p [112/100]² - p - 24p/100 = 72

p [12544/10000 - 1 - 24/100] = 72

p = 72 x 10000/144 = Rs. 5000

For the first year, there is no difference between simple interest and compound interest on any amount. Because compound interest is calculated over the interest from the first year as well, the second year's interest is different.

Hence, we can say that Rs. 72 = Interest on the first year's interest à 12% on the first year's interest = Rs. 72. Hence, the first year's interest = Rs. 600 which should be 12% of the original capital. Hence, original capital = Rs. 5000

Difference between Simple Interest and Compound Interest