Difference between Simpson's 1/3 rule and Trapezoidal Rule

In this article, we will understand the differences between the Simpson's 1/3 rule and Trapezoidal Rule.

Simpson's 1/3 rule:

This method is also called parabolic rules. In Simpson's 1/3 rule, we approximate the polynomial based on quadratic approximation. In this, each approximation actually covers two of the subintervals. This is why we require the number of subintervals to be even. Some of the approximations look more like a line than a quadric, but they really are quadratics

Following is the Formula of Simpson's ¹/₃ rule

ₐ∫ᵇ f (x) dx = h/₃ [(y₀ + yₙ) + 4 (y₁ + y₃ + ..) + 2(y₂ + y₄ + ..)]

In this,

a and b is the interval of integration

h = (b - a) / n

y₀ means the first terms and yₙ means the last terms.

(y₁ + y₃ + ..) means the sum of odd terms.

(y₂ + y₄ + …) means sum of even terms.

Example: Find the Solution using Simpson's 1/3 rule.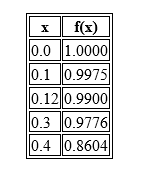

Solution:

By using Simpson's 1/3 rule

ₐ∫ᵇ f (x) dx = h/₃ [(y₀ + yₙ) + 4 (y₁ + y₃ + …) + 2 (y₂ + y₄ + …)]

h = 0.1

ₐ∫ᵇ f (x) dx = 0.1/3 [(1+0.8604)+4×(0.9975+0.9776)+2×(0.99)]

ₐ∫ᵇ f (x) dx = 0.1/3 [(1+0.8604)+4×(1.9751)+2×(0.99)]

ₐ∫ᵇ f (x) dx = 0.39136

Solution of Simpson's 1/3 rule = 0.39136

Trapezoidal Method

This method is also known as the trapezium rule. In the trapezoidal rule, we approximate the curve with a straight line and hence can only be accurate for sufficiently small h. This rule gives the exact value of the integral of f(x) as a linear function. when several trapezoids are used, we call it the composite trapezoidal rule.

Following is the Formula of Trapezoidal Method

ₐ∫ᵇ f (x) dx = h/2 [(y₀ + yₙ) + 2(y1+ y2 + ..)]

In this,

a and b is the interval of integration

h = (b - a)/ n

y₀ means the first terms and yₙ means the last term.

(y₁ + y2 + ..) means the sum of remaining terms.

Example: Find the Solution using Trapezoidal Method

Solution:

By using Trapezoidal Method

ₐ∫ᵇ f (x) dx = h/2 [(y₀ + yₙ) + 2(y1+ y2 + ..)]

h = (0.5 - 0) = (1 - 0.5) = (1.5 - 1) = 0.5

= (.5/2) [5 + 11 + 2 (6 + 9)]

= 0.25 [16+30]

= 0.25 [46]

= 11.5

Solution of Trapezoidal Method = 11.5

Following are the differences between Simpson's 1/3 rule and Trapezoidal Rule

	Simpson's 1/3 rule Method	Trapezoidal Method
1.	In Simpson's 1/3 rule Method, we approximate only the quadratic polynomial i.e. the parabolic curves.	In trapezoidal method, the boundary between the ordinates is straight.
2.	In Simpson 's 1/3 rule Method , the number of divisions should be even in this case.	In trapezoidal, there is no limitation, it is applicable for any number of ordinates.
3.	This method gives an approximate result.	This method gives an accurate results.
4.	The result obtained by Simpson's 1/3 rule Method rule are greater or lesser as the curve of the boundary is convex or concave towards the baseline.	The result obtained by the trapezoidal rule are not affected because the boundary between the ordinates is considered straight.
5.	In this method, chances of errors is more.	In this method, chance of errors is less.
6.	Computations are not as complex in this method.	Computations are complex in this method.
7.	The integral function can be calculated as = h/3 [(sum of 1st and last ordinates) + 4 (sum of odd ordinates) + 2 (sum of even ordinates)].	The integral function can be calculated as = h/2 [(sum of 1st and last ordinates) + 2 (sum of remaining ordinates)].
8.	Estimation in truncation error in Simpsons 1/3 rule is E< -nh5/180 y iv(x) where h = (b-a)/n	Estimation in truncation error in trapezoidal rule is E< -nh3/12 y iv(x) where h = (b-a)/n