Directed and Undirected graph in Discrete Mathematics

To learn the directed graph and undirected graph in discrete mathematics, we will first learn about the graph. After that, we will learn about the directed graph and undirected graph. The graph is described as follows:

Graph

The graph is a mathematical and pictorial representation of a set of vertices and edges. It consists of the non-empty set where edges are connected with the nodes or vertices. The nodes can be described as the vertices that correspond to objects. The edges can be referred to as the connections between objects. Arrow (→) is used to represent the edges. According to the direction of arrow, the graph will traverse. The edge of the graph sometimes contains the Weights, which is used to show the strength of each connection between vertices.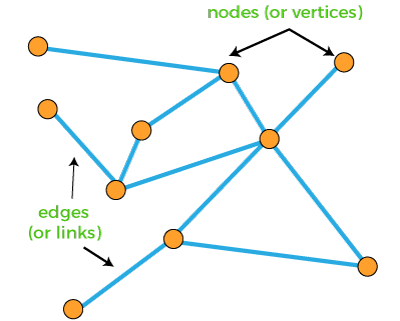

There are different formal definitions for different types of graphs on the basis of the edge. Because of this, various terminologies are created. In various applications, the nodes and edges have different definitions. For example: with the help of a graph, we can model the friendship of a social network, for instance. In the graph, the people will be represented with the help of nodes, and friendship will be represented with the help of edges.

With the help of a graph, we are able to model a wide variety of systems. Airports and Web page linking are a good example of it. In case of Airports, the airports will be represented by the nodes and lights between airports will be represented by the edges. While using a graph, there are some definitions that we should know about them and will be useful for us. These definitions are described as follows:

• The self-loop can be described as an edge that connects a vertex to itself. The sub-graph is a type of subset of the directed graph's edge that constitutes a directed graph.
• If two edges of a graph connect with the same ordered pair of vertices, these edges will be in parallel. The number of an edge can also be known as the length of a cycle or path. The out-degree of a vertex can be described as the number of edges pointing from it. The in-degree of a vertex can be described as the number of edges pointing to it.
• The directed path in a directed graph can be described as a sequence of vertices and a directed edge. Where, the edge is pointing from each vertex in the sequence to its successor in the sequence. The directed path will not contain repeated edges. If there are no repeated vertices, then the directed path will be simple.
• If the first and last vertices in the directed path are the same, and contain at least one edge, then the directed path will be known as the directed cycle. If there are no repeated vertices in the directed cycle except the requisite repetition of the first and last vertices, then the directed cycle will be simple. If there are no directed cycles, the directed graph will be known as the directed acyclic graph (DAG).
• Suppose there are two vertices, 'x' and 'y'. If there is a directed path from 'x' to 'y', then the vertex 'x' is reachable from vertex 'y'. If the vertices 'x' and 'y' both are mutually reachable, the vertices will be known as strongly connected. The mutually connected means that the vertex 'x' has a directed path from vertex 'y' and vertex 'y' also has a directed path from vertex 'x'.
• If every vertex has a directed path to every other vertex, the directed graph will be strongly connected. If the directed graph is not strongly connected, it will contain a set of strongly connected components. These types of components are maximal, strongly connected sub-graphs.

Types of Graph:

Now we will describe the two types of graph: Directed graph, undirected graph.

Directed Graph:

The directed graph is also known as the digraph, which is a collection of set of vertices edges. Here the edges will be directed edges, and each edge will be connected with order pair of vertices. In a graph, the directed edge or arrow points from the first/ original vertex to the second/ destination vertex in the pair. In the V-vertex graph, we will represent vertices by the name 0 through V-1. If there are two vertices, x and y, connected with an edge (x, y) in a directed graph, it is not necessary that the edge (y, a) is also available in that graph.

According to the definition of a directed graph, the same source and destination nodes are not allowed to have more than one arrow, but border definition is considered by some authors, which say that the same source and destination nodes can contain multiple arrows in the directed graph because they allow the arrow set to be a multiset. More specifically, we can address these types of entities as directed multigraphs.

On the basis of the aforementioned definition of a directed graph, a digraph is allowed to have loops. That means they can contain the arrows which directly connects nodes to themselves. If the directed graph has loops, that graph will be known as the loop digraph. In the following directed graph, there are only directed edges. It contains a directed edge from one vertex to any other vertex and a loop.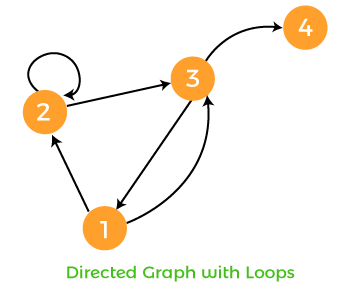

A narrower definition is allowed by some authors, which says that the digraph is not allowed to contain the loops. More specifically, if the digraph does not have the loops, that graph will be known as the simple directed graph. In the following directed graph, there are only directed edges. It contains a directed edge from one vertex to any other vertex, and it is not allowing looping.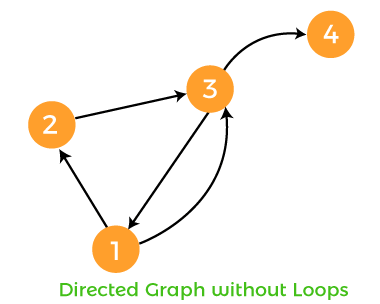

So we can say that a simple digraph does not have any type of loops, while any state is able to contain the multiple vertices (transitions) to multiple states. So in the vertices x and y, the directed graph can only do one transition from vertex x to vertex y, or vice versa.

Example 1:

In this example, the graph is able to traverse from vertex X to vertex Y, but it will not traverse from vertex Y to vertex X.

Example 2:

In this example, we will consider the following graph where G = {N, E}. Now we have to find out the vertex and edges set in this graph.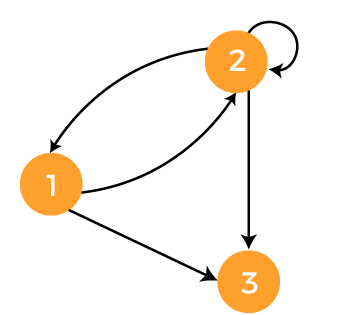

For the above graph, the vertex set and edge set is described as follows:

G = {{1, 2, 3}, {(1, 2), (2, 1), (2, 2), (2, 3), (1, 3)}}

Example 3: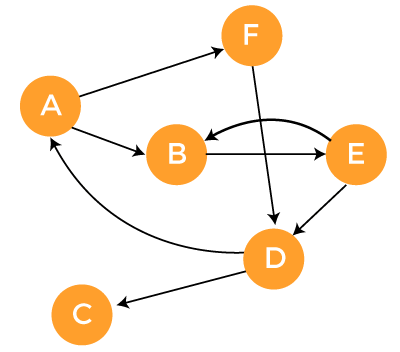

The Adjacent matrix for the above-directed graph is described as follows: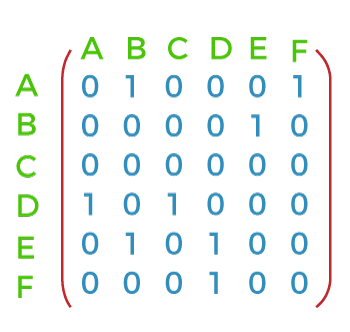

The adjacency list for a directed graph is described as follows: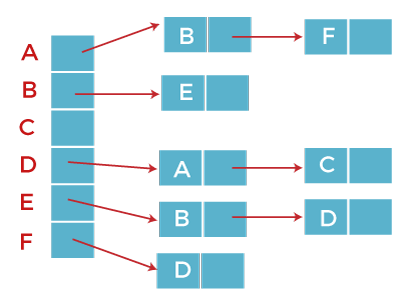

Undirected Graph

The undirected graph is also referred to as the bidirectional. It is a set of objects (also called vertices or nodes), which are connected together. Here the edges will be bidirectional. The two nodes are connected with a line, and this line is known as an edge. The undirected graph will be represented as G = (N, E). Where N is used to show the set of edges and E is used to show the set of edges, which are unordered pairs of elements N. The main difference between the directed and undirected graph is that the directed graph uses the arrow or directed edge to connect the two nodes. The arrow points from the original vertex to destination vertex in the directed graph. While in the undirected graph, the two nodes are connected with the two direction edges.

The undirected graph is more restrictive as compared to the directed graph because if the relationships have a hierarchical nature, then an undirected graph will not allow modeling them. The undirected graph is very common in practice. With the help of undirected graphs, we can easily model many real-world relationships. The relationship "is a friend of" can be called the typical symmetric relationship, for instance. This relationship is symmetric because if there is a case that "Mary is a friend of Harry", then "Harry is a friend of Mary" is also true.

Example 1:

In this example, the graph is able to traverse from vertex X to vertex Y, and it will also traverse from vertex Y to vertex X. It can traverse in both directions.

Example 2:

In this example, we will assume a graph where G = {N, E}. Where N = {1, 2, 3, 4}, and E = {(1, 2), (1, 4), (3, 4), (2, 3)}. Now we have to draw a graph for these vertices and edges.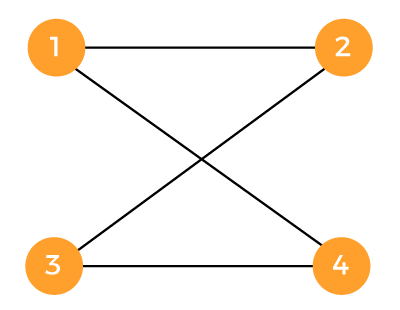

There is another way to draw the undirected graph with the help of given vertices and edges: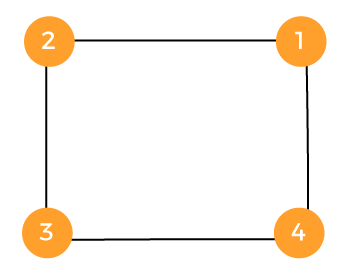

Example 3: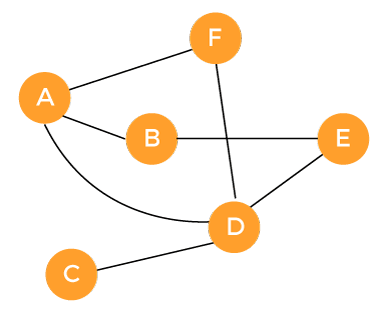

The Adjacent matrix for the above-undirected graph is described as follows: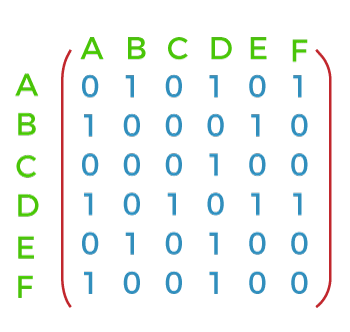

The adjacency list for an undirected graph is described as follows: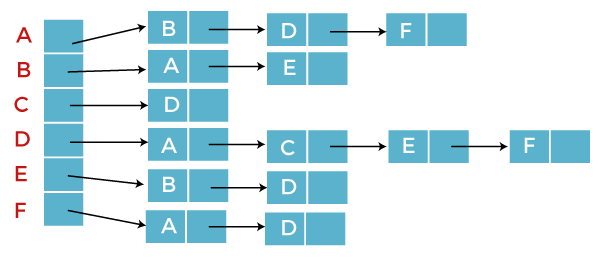

In the field of computer science, the most popular undirected graph can be expressed by the topology of connections in a computer network. If one system in a graph is connected to the other system, then the second system will also be connected with the first system in an undirected graph.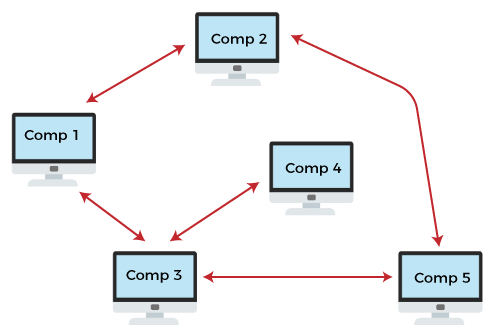

The topology of digital social networks is also a famous example of an undirected graph. Where, each friend of someone is that someone's friend. But there is also a pedestrian pathway. That means the two intersections of paths is able to move in both directions.

Selection between Directed Graph and Undirected Graph

Here we will describe some points that will help us choose either a directed graph or an undirected graph.

If the network is sparse, in this case, the directed graphs will be more informative as compared to the corresponding undirected graphs. This means that if the sparse directed graph is treated as undirected, the chances of losing the information are increased.

The relationships which are not reciprocal in nature and also directional can be modeled by the directional graphs. A relationship "is a child of" is a famous example of a directed graph because, with the help of this relationship, we can construct the genealogical trees.

The undirected graph is used to model those types of relationship for which it is important that the graph is existed or not, but they are not intrinsically transitive. Pedestrian paths are a good example of an undirected graph because, in pedestrian paths, we can go in both ways. That's why with the help of an undirected graph, the pathways are able to model.

In some circumstances, we can model the same system with the help of a directed graph. In another case, it will be modeled as an undirected graph. If we are learning progeny, the family can be represented with the help of a directed graph. In another case, if we are interested in learning clan affiliations, it can be represented with the help of an undirected graph.

The programmer has to carefully select between the directed and undirected graph according to the problem because both the graphs are mathematical abstractions over real-world phenomena. On the basis of the relation, we will use the graph to model it. If it is reciprocal, then we will use the undirected graph. Otherwise, we will use the directed graph.