Linear Search vs Binary Search

Before understanding the differences between the linear and binary search, we should first know the linear search and binary search separately.

What is a linear search?

A linear search is also known as a sequential search that simply scans each element at a time. Suppose we want to search an element in an array or list; we simply calculate its length and do not jump at any item.

Let's consider a simple example.

Suppose we have an array of 10 elements as shown in the below figure: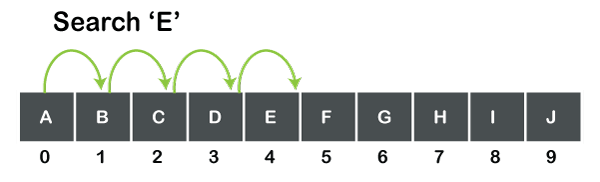

The above figure shows an array of character type having 10 values. If we want to search 'E', then the searching begins from the 0^th element and scans each element until the element, i.e., 'E' is not found. We cannot directly jump from the 0^th element to the 4^th element, i.e., each element is scanned one by one till the element is not found.

Complexity of Linear search

As linear search scans each element one by one until the element is not found. If the number of elements increases, the number of elements to be scanned is also increased. We can say that the time taken to search the elements is proportional to the number of elements. Therefore, the worst-case complexity is O(n)

What is a Binary search?

A binary search is a search in which the middle element is calculated to check whether it is smaller or larger than the element which is to be searched. The main advantage of using binary search is that it does not scan each element in the list. Instead of scanning each element, it performs the searching to the half of the list. So, the binary search takes less time to search an element as compared to a linear search.

The one pre-requisite of binary search is that an array should be in sorted order, whereas the linear search works on both sorted and unsorted array. The binary search algorithm is based on the divide and conquer technique, which means that it will divide the array recursively.

There are three cases used in the binary search:

Case 1: data<a[mid] then left = mid+1.

Case 2: data>a[mid] then right=mid-1

Case 3: data = a[mid] // element is found

In the above case, 'a' is the name of the array, mid is the index of the element calculated recursively, data is the element that is to be searched, left denotes the left element of the array and right denotes the element that occur on the right side of the array.

Let's understand the working of binary search through an example.

Suppose we have an array of 10 size which is indexed from 0 to 9 as shown in the below figure:

We want to search for 70 element from the above array.

Step 1: First, we calculate the middle element of an array. We consider two variables, i.e., left and right. Initially, left =0 and right=9 as shown in the below figure: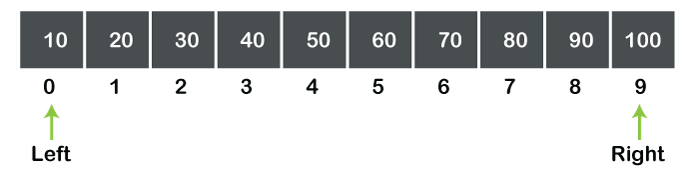

The middle element value can be calculated as: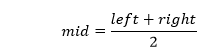

Therefore, mid = 4 and a[mid] = 50. The element to be searched is 70, so a[mid] is not equal to data. The case 2 is satisfied, i.e., data>a[mid].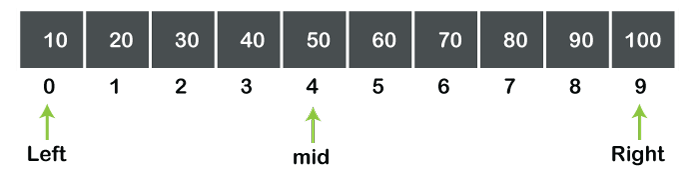

Step 2: As data>a[mid], so the value of left is incremented by mid+1, i.e., left=mid+1. The value of mid is 4, so the value of left becomes 5. Now, we have got a subarray as shown in the below figure: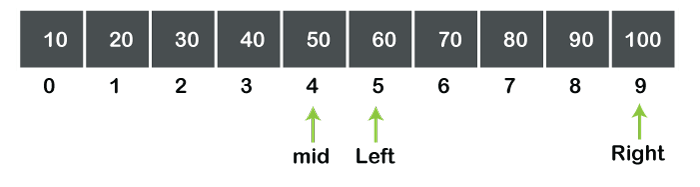

Now again, the mid-value is calculated by using the above formula, and the value of mid becomes 7. Now, the mid can be represented as: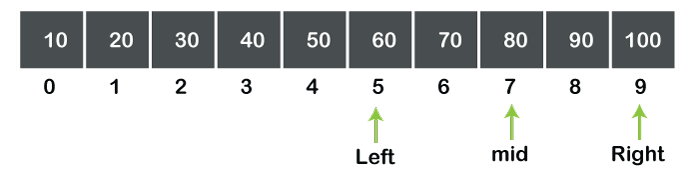

In the above figure, we can observe that a[mid]>data, so again, the value of mid will be calculated in the next step.

Step 3: As a[mid]>data, the value of right is decremented by mid-1. The value of mid is 7, so the value of right becomes 6. The array can be represented as: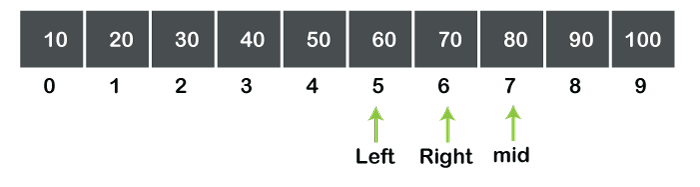

The value of mid will be calculated again. The values of left and right are 5 and 6, respectively. Therefore, the value of mid is 5. Now the mid can be represented in an array as shown below: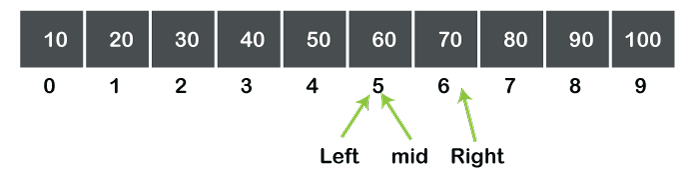

In the above figure, we can observe that a[mid]<data.

Step 4: As a[mid]<data, the left value is incremented by mid+1. The value of mid is 5, so the value of left becomes 6.

Now the value of mid is calculated again by using the formula which we have already discussed. The values of left and right are 6 and 6 respectively, so the value of mid becomes 6 as shown in the below figure: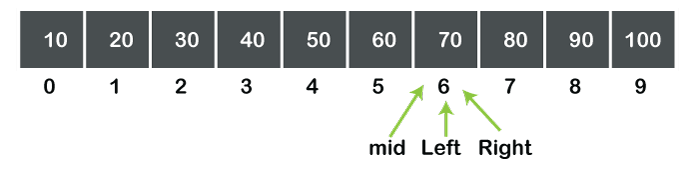

We can observe in the above figure that a[mid]=data. Therefore, the search is completed, and the element is found successfully.

Differences between Linear search and Binary search

The following are the differences between linear search and binary search:

Description

Linear search is a search that finds an element in the list by searching the element sequentially until the element is found in the list. On the other hand, a binary search is a search that finds the middle element in the list recursively until the middle element is matched with a searched element.

Working of both the searches

The linear search starts searching from the first element and scans one element at a time without jumping to the next element. On the other hand, binary search divides the array into half by calculating an array's middle element.

Implementation

The linear search can be implemented on any linear data structure such as vector, singly linked list, double linked list. In contrast, the binary search can be implemented on those data structures with two-way traversal, i.e., forward and backward traversal.

Complexity

The linear search is easy to use, or we can say that it is less complex as the elements for a linear search can be arranged in any order, whereas in a binary search, the elements must be arranged in a particular order.

Sorted elements

The elements for a linear search can be arranged in random order. It is not mandatory in linear search that the elements are arranged in a sorted order. On the other hand, in a binary search, the elements must be arranged in sorted order. It can be arranged either in an increasing or in decreasing order, and accordingly, the algorithm will be changed. As binary search uses a sorted array, it is necessary to insert the element at the proper place. In contrast, the linear search does not need a sorted array, so that the new element can be easily inserted at the end of the array.

Approach

The linear search uses an iterative approach to find the element, so it is also known as a sequential approach. In contrast, the binary search calculates the middle element of the array, so it uses the divide and conquer approach.

Data set

Linear search is not suitable for the large data set. If we want to search the element, which is the last element of the array, a linear search will start searching from the first element and goes on till the last element, so the time taken to search the element would be large. On the other hand, binary search is suitable for a large data set as it takes less time.

Speed

If the data set is large in linear search, then the computational cost would be high, and speed becomes slow. If the data set is large in binary search, then the computational cost would be less compared to a linear search, and speed becomes fast.

Dimensions

Linear search can be used on both single and multidimensional array, whereas the binary search can be implemented only on the one-dimensional array.

Efficiency

Linear search is less efficient when we consider the large data sets. Binary search is more efficient than the linear search in the case of large data sets.

Let's look at the differences in a tabular form.