Dynamic Programming interview questions

1) What is Dynamic programming?

The idea behind using the dynamic programming is that we have solved a problem with a given input then save the result for the future reference to avoid solving the same problem again and again. The dynamic programming was developed by Richard Bellman.

The dynamic programming in a dynamic programming world is a powerful technique that allows one to solve different types of problems in polynomial time for which a na�ve approach would take an exponential time.

For example, if we take the example of Fibonacci series in which each number is the sum of the next two preceding numbers. The Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, and so on. If we are asked to calculate the nth Fibonacci number. We can calculate this with the following recurrence formula:

Fib(n) = n if n<2

fib(n-1) + fib(n-2) otherwise

In the case of naive approach, the implementation of Fibonacci function has the time complexity of O(2^n) time where the dynamic programming approach solution can achieve the same with only O(n) time.

2) What are the characteristics of dynamic programming?

The following are the characteristics of dynamic programming:

• Optimal Substructures: If the overall optimal solution is evaluated from the optimal solutions of all the subproblems then the problem is said to be a optimal substructure property.
• Overlapping subproblems: When the larger problem is broken down into smaller problems then these smaller problems are known as subproblems. Let's consider an example of evaluating Fib(4) number. The Fib(4) is calculated by adding the values of Fib(3) and Fib(2), Fib(3) is calculated by adding Fib(2) and Fib(1) and Fib(2) is calculated by adding

3 What are the dynamic programming methods?

We can use the following two methods to optimize the problem:

• Top-down approach
• Bottom-up approach

Top-down approach

• The top-down approach is the technique to solve the larger problems by recursively finding the solution to the smaller problems.
• When the solution to the subproblem is found, then the result to the problem is stored or cache so that we do not need to calculate the result many times. Instead of calculating the result, we just have to return the cached result.
• The method of storing the result of already solved subproblems is known as a memorization.

Let's understand this approach with memorization and without memorization.

Without memoization

In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of 'n' increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2ⁿ.

With memorization

In the above code, we have declared an array named as 'memo'. We have declared this array so that we can store the result of the subproblem. This solves the problem of calculating the solution of already calculate subproblem.

4) What are the applications of dynamic programming?

The following is the list of applications of a dynamic programming:

• Google maps: Consider an example that we have to go from home to office every day. On the first day, we will calculate the shortest path by considering all the possible routes. Its not possible to recompute the shortest path every day so we memorize the shortest path. Google maps uses the dynamic programming approach to determine the shortest path between the source and the destination.
• Longest common subsequence: Here, longest means that it should be the largest among all the subsequences. Common means that two strings would be given and we have to find the common among the two subsequences. Subsequence is a sequence of characters from the string, and this sequence of characters should be in the increasing order with respect to their position.
  How can we create the subsequences?
  Consider the following example:
  W = a b c d
  = ab, bd, ac, ad, bd, acd, bcd, abcd
  The above are the subsequences that can be made with a string 'a b c d'. The subsequences ca, db are wrong as the subsequences should be made in the increasing order of their positions. As 'c' character appears after 'a' in the string so 'ca' subsequence is not possible. As 'd' character appears after 'b' in the string so 'db' subsequence is not possible. The total number of subsequences to be possible from the string would be 2n
  where 'n' is the number of characters in the string.
• Longest increasing subsequence problem: The longest increasing subsequence problem is a problem used to find the longest subsequence from the given sequence such that all the elements in a subsequence are sorted in an increasing order.
• Knapsack problem: In the divide-and-conquer strategy, the problem is divided into subproblems and these subproblems are further divided into subproblems. This process of division will continue till we achieve the subproblem which can be solved easily. In this process, we may encounter the same subproblems multiple times.
  The solution to the above problem is to use the technique of knapsack dynamic programming. The idea behind using the knapsack problem is to store the solutions in a table of already solved subproblems. If we face the same subproblem again, we just have to take out the solution of the subproblem from the table without solving it again. Therefore, we can say that the dynamic programming algorithms are quite effective.
  The following are the tasks need to be performed to solve the problem:
• First, we will find the solution to the subproblems.
• Then, we will find the formula to build the solution for the subproblem.
• In this step, we will create a table that will store the solutions of subproblems. Calculate the solution of the subproblems and stores the solution in a table.
• Once all the subproblems are solved, we will find the solution to the original problem.

5) What are the differences between the top-down approach and the bottom-up approach?

The following is the list of differences between the top-down approach and the bottom-up approach:

6) What are the differences between the dynamic programming and greedy approach?

The following is the list of differences between the dynamic programming and greedy approach:

7) What are the differences between the dynamic programming and divide and conquer approach?

The following is the list of differences between the dynamic programming and divide and conquer approach:

8) How dynamic programming is different from the memoization and recursion?

Recursion is a process of calling the function itself again and again. Memoization is a technique of storing the solution of solved sub problems. Dynamic programming is a technique of solving the recursions by storing the solutions of already sub problems.

9) What is the longest palindromic sequence?

The longest palindromic sequence is the problem where the sequence is given and we need to find the length of the longest palindromic subsequence. A subsequence is a sequence derived from the main sequence by taking some or all the elements from the sequence without changing the order of the elements. Here, the palindromic subsequence means that the elements appear same from both the directions, i.e., forward and backward direction.

Let's understand this problem through an example.

Suppose we have an input "bbbab".

The following are the palindromic subsequences that can be made from the above sequence:

bbbb

bbb

bab

Since the subsequence "bbbb" contains a greater number of characters, i.e., 4; therefore, the longest palindromic subsequence is "bbbb".

10) Problem statement:

Given two strings s1 and s2. We have to find the longest common subsequence between the strings s1 and s2.

For example:

S1: "ACBEA"

S2: "ADCA"

To start with this problem, let's match the strings character by character from the ends of the strings.

LCS("ACBEA", "ADCA") = 1 + LCS("ACBE", "ADC")

Since the character 'A' is common in the both the strings so we trim out the character 'A' from both the strings. We put 1 plus LCS of "ACBE" and "ADC". So, when the characters match, we trim that matched character and find out the LCS of the remaining strings. We put 1 because both the characters are matched.

LCS("ACBE", "ADC") = max(LCS(ACB, ADC), LCS(ACBE, AD))

In the above case, both the characters, i.e., 'E' and 'C' are different. So, first we leave the character from the string ACBE then we compute the LCS. Then, we remove the character from the string ADC. At the end, we consider the maximum of the above two LCSs.

Here we have followed two rules which are given below:

• If the characters are matched then we add the 1 and remove the matched characters.
• If the characters are not matched then we leave the character and compute the max of the LCSs.

The above approach can be implemented either recursively or using dynamic programming approach. Since recursive approach includes lots of comparisons that leads to the exponential complexity, so it is better to use a dynamic programming approach.

We consider the following tables:

Pointer table

The above is a pointer table where we keep the movements of the matching table. We will use this pointer table to generate the LCS of strings.

The following are the rules that we use here:

• Last chars match: We will trim the matching chars from both the strings and then add 1 to the LCS of the trimmed strings.
• Last chars mismatch: We will trim the one character at a time and then take the maximum of the LCS of both the combinations.

Let's start working on these matrices through the initialization.

First, we initialize both the matrices with zero.

Now we start with a first row. Since 'A' of both the strings are matched, so add 1 in the first table. We are trimming the character from both the strings so we can pick any of the strings either s1 or s2.

Trimming 'D' character

In the above case, we increment the count and move ahead. Now the strings which are into consideration are A and AD. Since both the characters, i.e., A and D do not match from both the strings so we can trim only one of the strings. If we trim A from the string s1 then we get an empty string and then we compare A and D in s2; the LCS of empty string and AD would be zero. If we trim D from the string s2 then the LCS of A, and AD would be 1 which is the LCS of A and A.

Since we are trimming character 'D' from the string s2, so we will add string s1 in column D in the pointer table. Here we are applying the rule that if we are trimming only one character at a time then if we trim s1 then we put s2 and if we trim s2 then we put s1 in the pointer table. If we are trimming both the characters then we can trim either s1 or s2.

Trimming 'C' character

Now, A and C are not matched so we increment a counter shown as below. Since we are trimming the character C from the string s2 so we add s2 under the column C in the pointer table. We move ahead to the column A.

Trimming 'A' character

In this case, A characters of both the strings are matched so we increment the counter shown as below. Here we are trimming the characters from both the strings, so we can add either s1 or s2. Once the counter is incremented, we move down.

Now the strings come into consideration are AC and A. If we trim A from the string s2 then we get an empty string; the LCS of empty string and AC would be zero. If we trim C from the string s1 then the LCS of A and AC would be equal to 1 shown as below. Once the counter is incremented, we move ahead.

Now the strings that come into consideration are AC and AD. In this case, we can trim either C or D. If we trim C then the LCS of A and AD is 1 and if we trim D then the LCS of AC and A is 1, so in both the case, the value of LCS is 1. Therefore, we can trim any of these strings, i.e., C and D. Suppose we remove the string C then the LCS of A and AD is 1 so we put 1 and s2 in the pointer table shown as below:

Now the strings that come into consideration are AC and ADC. Since both the characters, i.e., C of both the strings are matched, so we have to trim both the strings. The LCS of AC and ADC is now equal to 1 plus LCS of A and AD. Since the LCS of A and AD is equal to 1, so LCS of AC and ADC would be equal to 2. Since we are trimming both the strings so we can add any of the strings in the pointer table shown as below:

Now the strings that come into consideration are AC and ADCA. Since both the characters, i.e., C and A of both the strings are different so we can trim either C or A. If we trim A then the LCS of AC and ADC is 2, and if we trim C then the LCS of A and ADCA is 1. We have to consider the maximum LCS. Here, the maximum LCS is 2; therefore, the LCS of AC and ADCA is equal 2. Here, we are trimming the string s2, so we need to add s1 in the pointer table shown as below:

The pointer moves down. Now the strings that come into consideration are ACB and A. Since both the characters, i.e., B and A are different so we can trim either B and A. If we trim A then it would lead to an empty string. If we trim B then the LCS of ACB and A is equal to the LCS of AC and A which is 1 shown as below. In this case, we are trimming the s1 string so we have to add s2 in the pointer table. The pointer moves ahead.

Now the strings that come into consideration are ACB and AD. Since both the characters, i.e., B and D do not match, so we can trim either B or D. If we trim B, then the LCS of AC and AD is 1 and if we trim D, the LCS of ACB and A is 1. In both the cases, the value of LCS is 1 so we can trim either of the strings. The LCS of ACB and AD would be equal to 1 shown as below:

Now the strings that come into consideration are ACB and ADC. Since both the characters, i.e., B and C do not match, so we can trim either B and C. If we trim B, then the LCS of AC and ADC is 2 and if we trim C, then the LCS of ACB, and AD is 1. Since 2>1; therefore, LCS of ACB and ADC is equal to 2.

Now the strings that come into consideration are ACB and ADCA. Since both the characters, i.e., B and A do not match, so we can trim either B and A. If we trim B then the LCS of AC and ADCA is 2 and if we trim A then the LCS of ACB and ADC is 2. Since both the LCS are same so we can trim any of the strings. The LCS of ACB and ADCA would be 2.

LCS of ACB and ADC is equal to 2.

The strings that come into consideration are ACBE and A. Since both the characters, i.e., E and A are different so we can trim either E or A. If we trim E, then the LCS of ACB and A is 1. If we trim A then we would get an empty string and LCS would become 0. Since 1>0; therefore, the LCS of ACBE and A would be equal to the LCS of ACB and A, i.e., 1.

The strings that come into consideration are ACBE and AD. Since both the characters, i.e., E and D are different so we can trim either E and D. If we trim E, then the LCS of ACB and AD is 1. If we trim D, then the LCS of ACBE and A is 1. Since both the LCS are same so we can trim any of these strings either ACBE or AD. Therefore, the LCS value of ACBE and AD is 1 and any string s1 or s2 can be added in the pointer table shown as below:

Now the strings that come into consideration are ACBE and ADC. Since both the characters, i.e., E and C are different so we can trim either E or C. If we trim E, then the LCS of ACB and ADC is 2. If we trim C, then the LCS of ACBE and AD is 1. Since 2>1; therefore, the LCS of ACBE and AD is equal to the LCS of ACB and ADC which is 2.

The strings that we consider now are ACBE and ADCA. Since both the characters, i.e., E and A are different so we can trim either E or A. If we trim E, then the LCS of ACB and ADCA is 2. If we trim A, then the LCS of ACBE and ADC is 1. Since 2>1; therefore, the LCS of ACBE and ADCA is equal to the LCS OF ACB and ADCA which is 2.

The strings that we consider now are ACBEA and A. Since both the characters match, i.e., A so we need to trim both the strings. The LCS value of ACBEA and A would be updated as 1 and any of the strings, i.e., s1 or s2 could be added in the pointer table shown as below:

The strings that we consider now are ACBEA and AD. Since both the characters, i.e., A and D do not match so we can trim either of the strings. If we trim D then the LCS value of ACBEA and A is 1. If we trim A then the LCS value of ACBE and AD is 1. Since the LCS value in both the cases is same, i.e., 1; therefore, the LCS value of ACBEA and AD is equal to 1. We can add any of the strings in the pointer table shown as below:

The strings that we consider now are ACBEA and ADC. Since both the characters, i.e., A and C are different so we can trim either of the strings. If we trim A, then the LCS value of ACBE and ADC is 2. If we trim C, then the LCS value of ACBEA and AD is 1. Since 2>1; therefore, the LCS value of ACBEA and ADC is equal to the LCS value of ACBE and ADC which is equal to 2. In the case, we are trimming s1 so we will add s2 in the pointer table shown as below:

The strings that we consider now are ACBEA and ADCA. Since both the characters, i.e., A of both the strings match, so we have to trim both the strings. Therefore, the LCS of ACBEA and ADCA is equal to (1 plus LCS of ACBE and ADC, i.e., 2) 3.

We conclude that the length of the longest common subsequence is 3. Now we have to determine the subsequence. The following are the rules used to determine the subsequence:

• If the pointer table contains s1/s2 strings then we have to go diagonally up.
• If the pointer table contains a string s1 then we have to go left.
• If the pointer table contains a string s2 then we have to go up.

Since the pointer is pointing to the last row and the last column, and the value is s1/s2. So, the pointer will move diagonally pointing to the string s2 shown as below: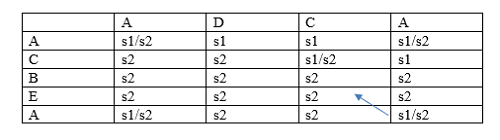

Now the pointer is pointing to the string s2 so pointer will move up and pointing to the string s2 shown as below: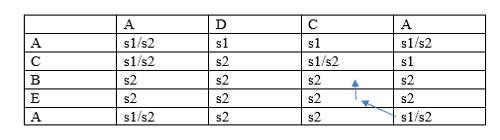

Since the pointer is pointing to the string s2 so pointer will move up and pointing to the string s1/s2 shown as below: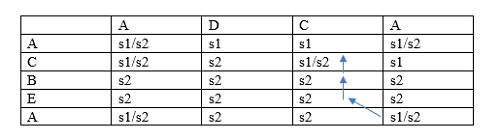

Since the pointer is pointing to the string s1/s2 so pointer will go diagonally up and pointing to the string s1 shown as below: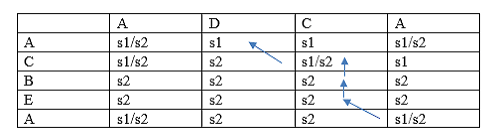

Since the pointer is pointing to the string s1 will move left and pointing to the string s1/s2 shown as below: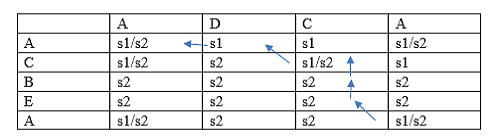

From the above table, we can observe that longest common subsequence is ACA.

11) What are the pros and cons of memoization or top-down approach?

Advantages

• It is very easy to understand and implement.
• It solves the subproblems only when it is required.
• It is easy to debug.

Disadvantages

It uses the recursion technique that occupies more memory in the call stack. Sometimes when the recursion is too deep, the stack overflow condition will occur.

It occupies more memory that degrades the overall performance.

12. Which approach should we consider when choosing between the top-down approach and the bottom-up approach solutions for the same problem?

The following are the two things that we consider while deciding an algorithm:

• Time complexity: Since both the approaches have the similar time complexity but for loop is cheaper than the recursive function calls. Therefore, we can say that bottom-up approach is faster than the top-down approach in terms of machine time.
• Space complexity: When we are not considering the extra call stack allocations during the top-down. Mainly both the approaches are used to build a table for all the sub-solutions but bottom-approach follows a topological order where the cost of auxiliary space can be reduced to the size of problem's immediate dependencies. For example, fibonacci(n)= fibonacci(n-1) + fibonacci(n-2), here we are storing only two previous calculations.