ELM in Machine Learning

Huang et al. introduced the Extreme Learning Machine (ELM), a machine learning method in 2006. It is a type of feedforward artificial neural network that can learn from input data with high accuracy and efficiency. ELM has gained popularity in recent years due to its ability to solve a wide range of real-world problems in various fields, such as image and speech recognition, data classification, and regression analysis.

Concept of ELM

ELM is a type of feedforward neural network that uses a single hidden layer with randomly generated weights and biases. Unlike other neural networks, ELM does not require iterative training or tuning of the weights and biases to achieve high accuracy. Instead, it uses an analytical solution to calculate the output weights based on the input data.

The training phase and the testing phase are the two phases of the ELM algorithm hidden layer's weights, and biases are created at random when the input data is fed into the neural network during the training phase. The output weights are then calculated using a least-squares method. The training process is fast and does not require any iterative adjustment of the weights and biases.

The input data is fed into the neural network during the testing phase, and the output is computed using the previously determined output weights. The output of the ELM algorithm is the same as that of other neural networks, which is a set of predicted values for each input.

Architecture of ELM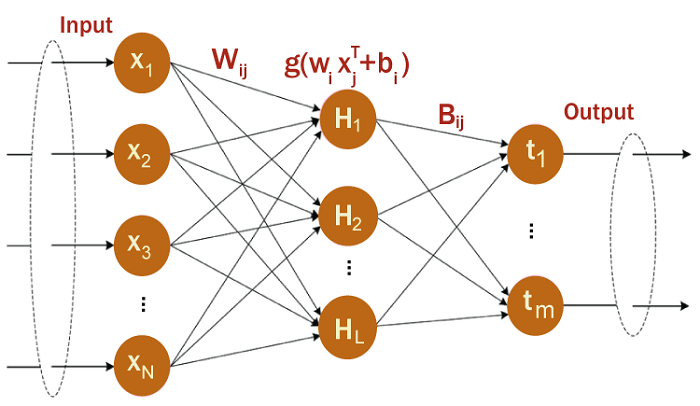

The architecture of ELM consists of three layers: the input layer, the hidden layer, and the output layer. The input layer receives the input data, which is usually a set of feature vectors. The hidden layer contains a set of randomly generated weights and biases, and the output layer produces the predicted values.

An essential element of the ELM is the buried layer's number of nodes. The complexity of the model and the precision of the predictions are influenced by the number of hidden nodes. In general, the more hidden nodes there are, the better the accuracy, but the more complex the model becomes. Finding the ideal quantity of hidden nodes for each issue is crucial.

ELM Training

Training an ELM is a relatively simple and efficient process. The training data is first preprocessed, and the input and output values are normalized to a suitable range. The hidden layer size is then specified, and the random weights between the input and hidden layer are generated. The non-linear mapping is performed using a suitable activation function, such as the sigmoid or the hyperbolic tangent function.

Once the hidden layer mapping is performed, the output weights are computed using a linear regression technique. Either the least squares approach or the Moore-Penrose pseudoinverse can be used to determine the output weights. The Moore-Penrose pseudoinverse is generally faster and more efficient than the least squares method, but it can be more prone to numerical instability. Once the output weights are computed, the output values can be computed using the output layer.

Advantages of ELM

• One of the main advantages of ELM is its fast-training speed. ELM does not require iterative training or tuning of the weights and biases, which makes it much faster than other neural networks. The training process can be completed in a single step, which significantly reduces the computational cost.
• Another advantage of ELM is its ability to handle high-dimensional data. ELM can efficiently process large datasets with thousands of features, which is a common problem in many real-world applications. The random weights and biases in the hidden layer allow ELM to avoid the curse of dimensionality, which is a major problem in traditional neural networks.
• ELM also has good generalization performance. ELM can achieve high accuracy on both the training and testing datasets, which indicates good generalization performance. This is because ELM does not overfit the data, as it does not rely on iterative training or tuning of the weights and biases.

Limitations of ELM

• One of the main limitations of ELM is that it may not always achieve the same level of accuracy as other neural networks, such as deep learning models. While ELM can achieve high accuracy on many problems, it may not be suitable for very complex problems that require deep architectures.
• Another limitation of ELM is its sensitivity to the number of hidden nodes. The optimal number of hidden nodes may vary depending on the problem, and selecting the wrong number of hidden nodes can lead to poor performance. Therefore, it is important to tune it carefully.

Applications of ELM

ELM has been applied to a wide range of machine-learning problems, including classification, regression, and clustering. ELM has been used in image and speech recognition, financial forecasting, and medical diagnosis. ELM has also been used in natural language processing, recommendation systems, and bioinformatics.

Conclusion

In conclusion, ELM is a powerful and efficient machine-learning algorithm that has gained widespread recognition in recent years. ELM is well-suited to handle a wide range of machine-learning problems, including classification, regression, and clustering. ELM has several advantages over other machine learning algorithms, including its speed, efficiency, and ability to handle high-dimensional and non-linear data. ELM has been applied to a wide range of real-life datasets.