Encoders

The combinational circuits that change the binary information into N output lines are known as Encoders. The binary information is passed in the form of 2^N input lines. The output lines define the N-bit code for the binary information. In simple words, the Encoder performs the reverse operation of the Decoder. At a time, only one input line is activated for simplicity. The produced N-bit output code is equivalent to the binary information.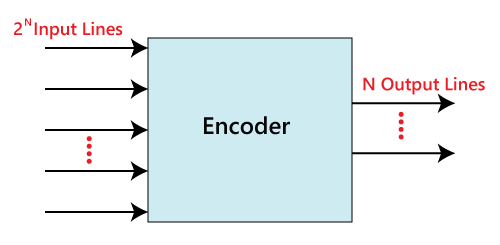

There are various types of encoders which are as follows:

4 to 2 line Encoder:

In 4 to 2 line encoder, there are total of four inputs, i.e., Y₀, Y₁, Y₂, and Y₃, and two outputs, i.e., A₀ and A₁. In 4-input lines, one input-line is set to true at a time to get the respective binary code in the output side. Below are the block diagram and the truth table of the 4 to 2 line encoder.

Block Diagram: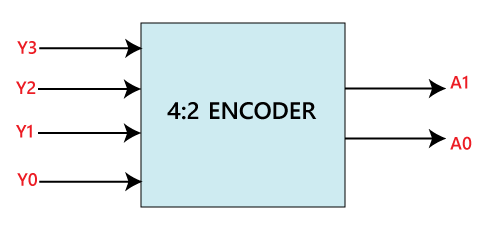

Truth Table: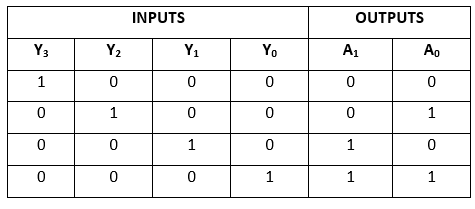

The logical expression of the term A0 and A1 is as follows:

A₁=Y₃+Y₂
A₀=Y₃+Y₁

Logical circuit of the above expressions is given below: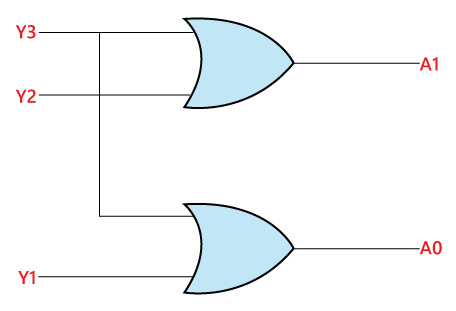

8 to 3 line Encoder:

The 8 to 3 line Encoder is also known as Octal to Binary Encoder. In 8 to 3 line encoder, there is a total of eight inputs, i.e., Y₀, Y₁, Y₂, Y₃, Y₄, Y₅, Y₆, and Y₇ and three outputs, i.e., A₀, A1, and A₂. In 8-input lines, one input-line is set to true at a time to get the respective binary code in the output side. Below are the block diagram and the truth table of the 8 to 3 line encoder.

Block Diagram: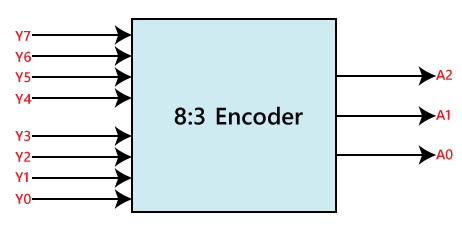

Truth Table: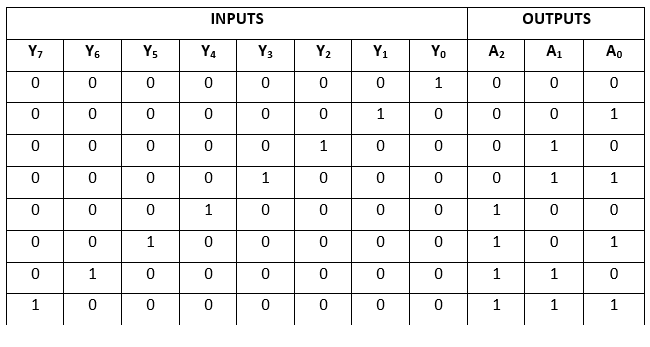

The logical expression of the term A0, A1, and A2 are as follows:

A₂=Y₄+Y₅+Y₆+Y₇
A₁=Y₂+Y₃+Y₆+Y₇
A₀=Y₇+Y₅+Y₃+Y₁

Logical circuit of the above expressions is given below: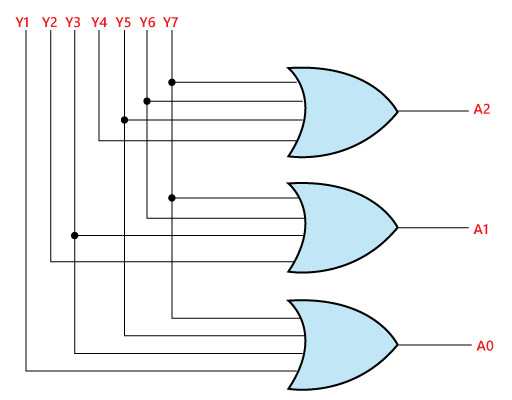

Decimal to BCD Encoder

The Octal to Binary Encoder is also known as 10 to 4 line Encoder. In 10 to 4 line encoder, there are total of ten inputs, i.e., Y₀, Y₁, Y₂, Y₃, Y₄, Y₅, Y₆, Y₇, Y₈, and Y₉ and four outputs, i.e., A₀, A1, A₂, and A₃. In 10-input lines, one input-line is set to true at a time to get the respective BCD code in the output side. The block diagram and the truth table of the decimal to BCD encoder are given below.

Block Diagram: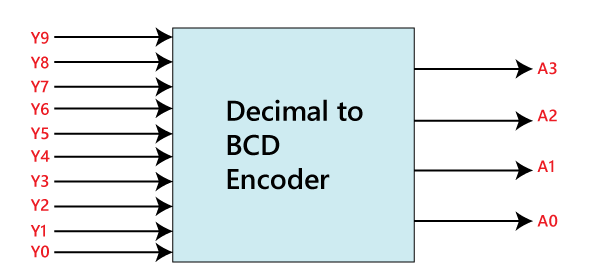

Truth Table: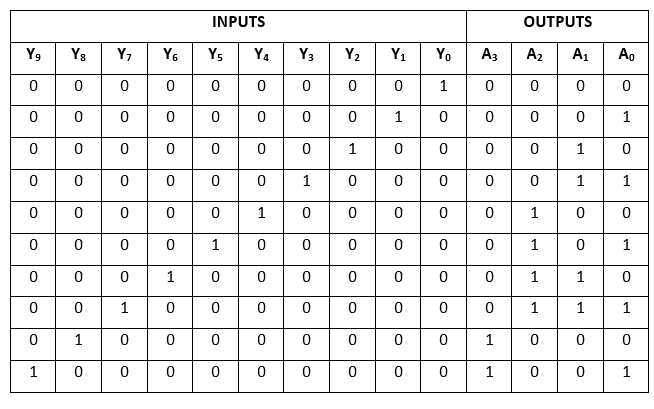

The logical expression of the term A₀, A₁, A₂, and A₃ is as follows:

A3 = Y9 + Y8
A2 = Y7 + Y6 + Y5 +Y4
A1 = Y7 + Y6 + Y3 +Y2
A0 = Y9 + Y7 +Y5 +Y3 + Y1

Logical circuit of the above expressions is given below: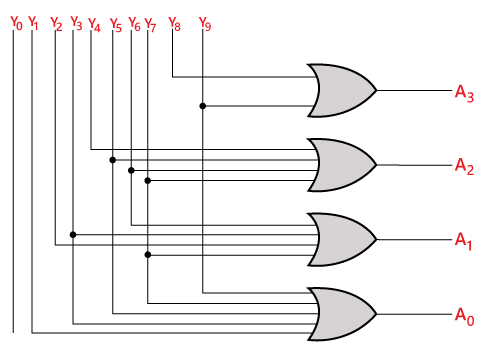

Priority Encoder:

4 to 2 line Priority Encoder:

In this priority encoder, there are total of 4 inputs, i.e., Y₀, Y₁, Y₂, and Y₃, and two outputs, i.e., A₀ and A₁. The Y₃ has high and Y₀ has low priority inputs. When more than one input is '1' at the same time, the output will be the (binary) code corresponding to the higher priority input. Below is the truth table of the 4 to 2 line priority encoder.

Truth Table: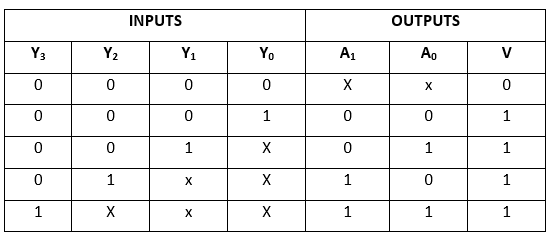

The logical expression of the term A₀ and A₁ can be found using K-map as: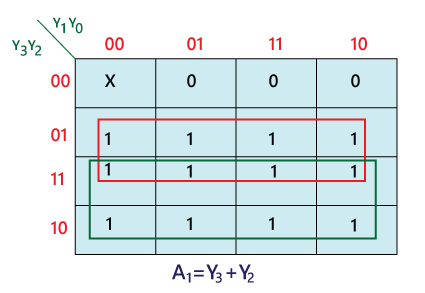

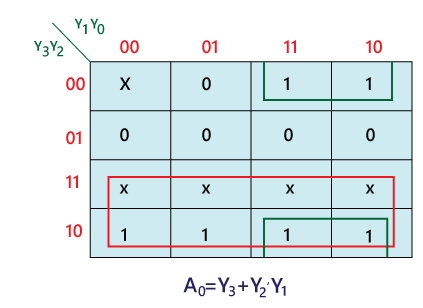
A₁=Y₃+Y₂
A₀=Y₃+Y₂'.Y₁

Logical circuit of the above expressions is given below: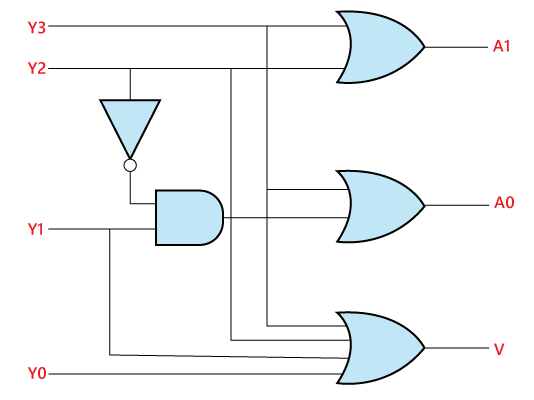

Uses of Encoders:

1. These systems are very easy to use in all digital systems.
2. Encoders are used to convert a decimal number into the binary number. The objective is to perform a binary operation such as addition, subtraction, multiplication, etc.