Equation Definition

The numbers on each side of the equal sign in an equation are equal.That is the definition of an equation in mathematics, but an equation may also be used to describe various problems, situations, or efforts to solve an issue. A well-formed formula consisting of two expressions linked by an equals sign is considered an equation in English. However, the word's cognates in other languages may have slightly different definitions. For instance, an equation is defined as having one or more variables in French.

Determine which benefits of the factors make the equity true to settle an equation with factors. Questions are another name for the factors that the equation must account for, and arrangements of the equation are another name for the benefits of the questions that satisfy the equity. Character equations and dependent equations are the two types of equations. All benefits of the elements apply to a character. A contingent equation only holds for particular advantages of the components.

An equation comprises two articulations associated with an equal sign ("="). The "left-hand side" and "right-hand side" in the equation refer to the articulations on the various sides of the equal sign. Frequently the right-hand side of an equation is thought to be zero. Expecting this doesn't diminish the consensus; this can be acknowledged by removing the right-hand side from the two sides.

The most frequent equation has two polynomial sides and is known as a polynomial or algebraic equation. A polynomial equation has one or more terms on each of its sides. For instance, the formula

Ax^2+Bx+C-y = 0

A scale on which weights are placed is a good analogy for an equation. Equal weights of material (like grain) are put into both pans until the scales are balanced, at which point the weights are considered equal. Grain removal from one of the balance's pans must be matched by removal from the other to maintain balance on the scale. A balance is generally maintained in an equation if an identical operation is carried out on both sides.

In Cartesian math, equations are utilized to depict mathematical figures. As the equations that are thought of, like verifiable or parametric equations, have boundlessly numerous arrangements, the goal is presently unique: rather than giving the arrangements unequivocally or counting them, which is inconceivable, one proposes equations for concentrating on properties of figures. This is the beginning thought of logarithmic calculation, a significant area of mathematics.

The two introductory algebra types studied are polynomial and the specific case of linear equations. When there is a single variable, temperate conditions have the structure hatchet a + b = 0, and polynomial conditions have the structure P(x) = 0, where P is a polynomial. Both families of problems can be solved using algorithmic or geometric methods that come from mathematical analysis or linear algebra. In algebra, Diophantine equations with integer coefficients and solutions are also studied. Different methods are employed that have their roots in number theory. These equations are generally challenging; thus, people frequently look for the presence or lack of a solution and, if one exists, the number of solutions.

Differential equations are those that involve one or more functions and their derivatives. By identifying a derivative-free formulation for the function, they may be resolved. Differential equations are used in fields including physics, chemistry, biology, and economics to represent processes involving the rates of change of the variable.

Robert Recorde created the "=" sign in 1557 because he believed that nothing could be more equal than two parallel straight lines of the same length. It has been used in every equation since then.

Analogous Illustration

The equation's two sides stand in for the balance's two sides. The scale will balance even if different weights are placed on either side because, by analogy, the equality that serves as the balance will also be balanced if the weights on the two sides are equal.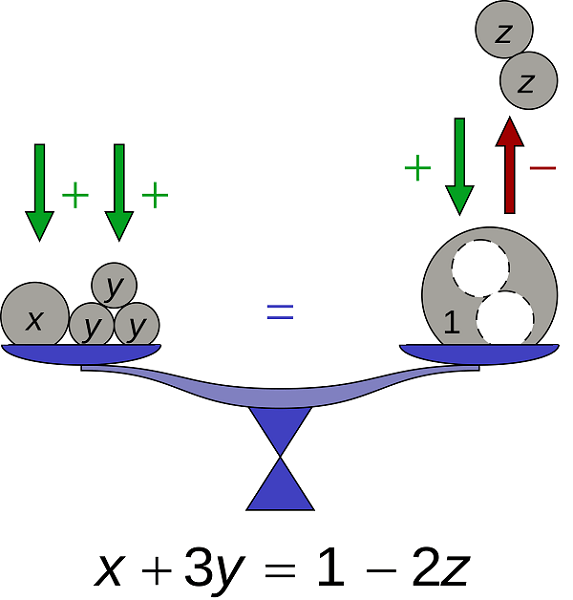

In the example, the three different values (in this case, real numbers) x, y, and z are each represented as circular weights, each having a distinct weight. Subtraction removes weight from what already exists, whereas addition adds weight to the system. When equality holds, both sides have the same overall weight.

Properties

Having the same set of solutions makes two equations or two systems of equations equal. The following processes change an equation or system of equations into an equivalent one, assuming that the operations are appropriate for the expressions they are applied to:

• By adding or removing, you can modify an equation's variables on all sides by the same amount. This demonstrates how every equation equals an equation whose right side is zero.
• A non-zero number multiplies or divides an equation's two sides.
• Applying an identity to one side of the equation to change it. Adding more to a product or factoring in a total are two examples.
• For a framework: adding the same side of another situation, increased by a similar sum, to the two sides of a situation.

When a function is applied to both sides of an equation, the new equation includes the original equation's solutions among its solutions but may also contain additional solutions known as superfluous solutions. For illustration, the equation x= 1 has the solution x= 1. The equation becomes x2 = 1, which displays the unnecessary answer and the previous solution, x = -1, by applying the function and elevating both sides to the exponent of 2. Furthermore, solutions for certain function values may be lost (for example, 1/x is not specified when x = 0). So, when using such a transformation on an equation, care must be used.

Geometry

Analytic Geometry

Each point in space can be given a set of coordinates in Euclidean geometry by using an orthogonal grid. Equations can be used with this technique to describe geometric shapes. One way to represent a plane in three dimensions is as the set of solutions to an equation of the form ax+by+cz+d = 0, where the real values a, b, c, and d are, and the unknowns x, y, and z are the coordinates of a point in the system determined by the orthogonal grid.

The letters a, b, and c represent a vector's coordinates perpendicular to the plane the equation suggests. A line is defined as the set of solutions to either a single linear equation with values in R2 or the set of solutions to two linear equations with values in R3, depending on where the two planes intersect.

An equation and a cone form a conic section x^2 + y^2 = z^2 and a plane. In other words, all conics are the solutions to the previously stated equations for a plane and a cone in space. With this formalization, it is possible to identify the locations and characteristics of a conic's foci.

Using equations permits one to approach a huge area of mathematics to tackle mathematical inquiries. The Cartesian direction framework changes a mathematical issue into an investigation issue when the figures are changed into equations; in this manner, the name is scientific calculation. This perspective, illustrated by Descartes, improves and adjusts the calculation the old Greek mathematicians imagined.

Analytic geometry indicates a current area in mathematics. It still utilizes equations to describe the pictures but employs more complex methods like functional analysis and linear algebra.

Cartesian Equations

Two numerical coordinates may uniquely identify any point in a plane; the signed distances between the point and two fixed perpendicular directed lines are indicated by the same unit of length. These distances are called Cartesian coordinates.

One can utilize a similar standard to determine the place of any point in a three-layered space by utilizing three Cartesian directions, which are the considerable distances to three commonly opposite planes (or, identically, by its opposite projection onto three commonly opposite lines).

Ren� Descartes (also known by his Latinized name, Cartesius), who discovered Cartesian coordinates in the 17th century, revolutionized mathematics by making the first systematic relationship between Euclidean geometry and algebra. Cartesian equations, which are algebraic equations involving the coordinates of the points on the form when using the Cartesian coordinate system, can be used to describe geometric forms (such as curves). For instance, the set of all points whose coordinates x and y meet the formula x2 + y2 = 4 may represent a circle of radius 2 in a plane centered on a specific point known as the origin.

Number Theory

Diophantine Equation

When only integer solutions are sought for a polynomial equation with two or more unknowns, the equation is said to be Diophantine (an integer solution is one in which all the unknowns have integer values). A linear Diophantine equation involves the sum of two monomials of degree 0 or 1. Ax + by = c, where a, b, and c are constants, illustrates a linear Diophantine equation. Exponents of the terms in an exponential Diophantine equation are variables that might be unknown.

Diophantine issues have fewer equations than unknown factors and include finding numbers that turn out accurately for all equations. In more specialized language, they characterize a mathematical bend, arithmetical surface, or more comprehensive article and get some information about the cross-section focused on it.

The term "Diophantine" refers to the Greek mathematician of the third century AD, Diophantus of Alexandria, who investigated such equations and may have been the first to introduce imagery to polynomial mathematics. The Diophantine examination is the modern name for the numerical exploration of Diophantus's problems.

Algebraic and Transcendental Numbers

An algebraic number is a number that is a non-no polynomial condition in one variable with objective coefficients (or with whole number coefficients by clearing the denominators). Transcendental numbers, such as those that cannot be expressed algebraically. Nearly all complex and real numbers are transcendental.

Algebraic Geometry

Algebraic geometry is a part of math, traditionally concentrating on arrangements of polynomial equations. Present-day algebraic geometry depends on additional theoretical methods of unique variable-based math, particularly commutative variable-based math, with language and geometry issues.

Algebraic varieties are geometric representations of polynomial equation systems that have been solved and are the basic study objects in algebraic geometry. The most researched classes of algebraic varieties are the Cassini ovals and planar algebraic curves, which include lines, circles, parabolas, ellipses, hyperbolas, and cubic curves like elliptic curves and quartic curves like lemniscates. If a point's coordinates match a specified polynomial equation, that point is said to belong to an algebraic curve. The study of specific points of interest, such as solitary points, inflection points, and points at infinity, is involved in fundamental concerns. Curve topology and relationships between curves provided by various equations are topics for more complex issues.

Differential Equations

A differential equation is any mathematical formula that links a function and its derivatives. Applications often use functions to represent physical quantities, derivatives to indicate the rates at which those values change, and an equation to express the connection between the two. Since such relationships are frequent, differential equations are widely used in many fields, including physics, engineering, economics, and biology.

Differential equations are examined in pure mathematics from various angles, with the main focus being on their solutions?the collection of functions that satisfy the equation. Only the simplest differential equations can be resolved with explicit formulae, but even without knowing an exact solution's form, it is possible to deduce some of an equation's characteristics.

In the absence of a self-contained formula, the answer can be quantitatively estimated with the use of computers. The dynamical systems theory strongly focuses on qualitatively studying systems characterized by differential equations. At the same time, several numerical techniques have been developed to find solutions with a certain level of precision.

Ordinary Differential equations

An ordinary differential equation (ODE) is an equation that has a function of one independent variable and its derivatives. The phrase "ordinary" describes differential equations as opposed to partial differential equations, which may have many independent variables.

Linear differential equations, which have arrangements that can be added and increased by coefficients, are obvious and perceived, and precise shut structure arrangements are obtained. On the other hand, Tributes that need added substance arrangements are nonlinear, and settling them is undeniably more mind-boggling, as one can seldom address them by rudimentary capabilities in shut structure: All things being equal, careful and logical arrangements of Tributes are in series or basic structure. Graphical and mathematical techniques, applied the hard way or by PC, may estimate arrangements of Tributes and maybe yield valuable data, frequently doing the trick without a trace of precise, logical arrangements.