Euler Graph in Discrete Mathematics

If we want to learn the Euler graph, we have to know about the graph. The graph can be described as a collection of vertices, which are connected to each other with the help of a set of edges. We can also call the study of a graph as Graph theory. In this section, we are able to learn about the definition of Euler graph, Euler path, Euler circuit, Semi Euler graph, and examples of the Euler graph.

Euler Graph

If all the vertices of any connected graph have an even degree, then this type of graph will be known as the Euler graph. In other words, we can say that an Euler graph is a type of connected graph which have the Euler circuit. The simple example of Euler graph is described as follows: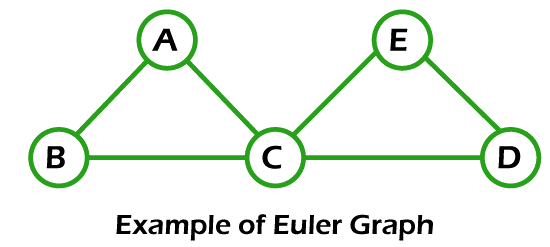

The above graph is a connected graph, and the vertices of this graph contain the even degree. Hence we can say that this graph is an Euler graph.

In other words, we can say that this graph is an Euler graph because it has the Euler circuit as BACEDCB.

Euler Path

We can also call the Euler path as Euler walk or Euler Trail. The definition of Euler trail and Euler walk is described as follows:

• If there is a connected graph with a trail that has all the edges of the graph, then that type of trail will be known as the Euler trail.
• If there is a connected graph, which has a walk that passes through each and every edge of the graph only once, then that type of walk will be known as the Euler walk.

Note: If more than two vertices of the graph contain the odd degree, then that type of graph will be known as the Euler Path.

Examples of Euler path:

There are a lot of examples of the Euler path, and some of them are described as follows:

Example 1: In the following image, we have a graph with 4 nodes. Now we have to determine whether this graph contains an Euler path.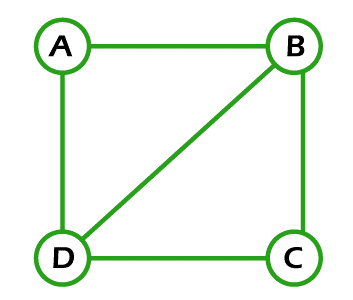

Solution:

The above graph will contain the Euler path if each edge of this graph must be visited exactly once, and the vertex of this can be repeated. So if we begin our path from vertex B and then go to vertices C, D, B, A, and D, then in this process, each and every edge is visited exactly once, and it also contains repeated vertex. So the above graph contains an Euler path, which is described as follows:

Example 2: In the following image, we have a graph with 6 nodes. Now we have to determine whether this graph contains an Euler path.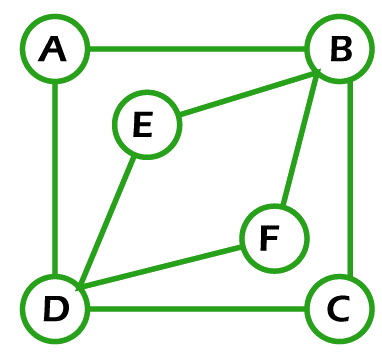

Solution:

The above graph will contain the Euler path if each edge of this graph must be visited exactly once, and the vertex of this can be repeated. So if we begin our path from vertex B and then go to vertices C, D, F, B, E, D, A, and B, then in this process, each and every edge is visited exactly once, and it also contains repeated vertex. So the above graph contains an Euler path, which is described as follows:

Example 3: In the following image, we have a graph with 5 nodes. Now we have to determine whether this graph contains an Euler path.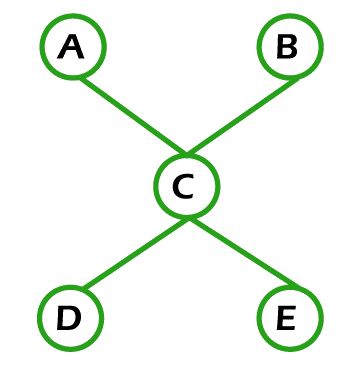

Solution:

The above graph will contain the Euler path if each edge of this graph must be visited exactly once, and the vertex of this can be repeated. So if we begin our path from A, then we can only go to vertex A, C, D or B, C, E. That means this graph cannot visit all the edges only once. So the above graph does not contain an Euler path.

Euler Circuit:

We can also call the Euler circuit as Euler Tour and Euler Cycle. There are various definitions of the Euler circuit, which are described as follows:

• If there is a connected graph with a circuit that has all the edges of the graph, then that type of circuit will be known as the Euler circuit.
• If there is a connected graph, which has a walk that passes through each and every edge of the graph only once, then that type of walk will be known as the Euler circuit. In this walk, the starting vertex and ending vertex must be the same, and this walk can contain the repeated vertex, but it is not compulsory.
• If an Euler trail contains the same vertex at the start and end of the trail, then that type of trail will be known as the Euler Circuit.
• A closed Euler trail will be known as the Euler Circuit.

Note: If all the vertices of the graph contain the even degree, then that type of graph will be known as the Euler circuit.

Examples of Euler Circuit

There are a lot of examples of the Euler circuit, and some of them are described as follows:

Example 1: In the following image, we have a graph with 4 nodes. Now we have to determine whether this graph contains an Euler circuit.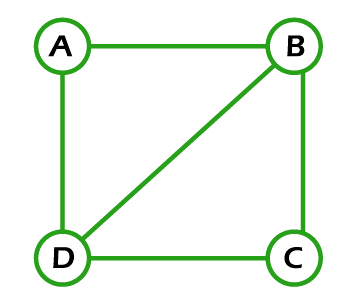

Solution:

The above graph will contain the Euler circuit if the starting vertex and end vertex are the same, and this graph visits each and every edge only once. The Euler circuit can contain the repeated vertex. If we begin our path from vertex A and then go to vertices B, C, D, and A, then in this process, the condition of same starting and end vertex is satisfied, but another condition of covering all edges is not satisfied because there is one edge from vertex D to B, which is not covered. If we try to cover this edge, then the edges will be repeated. So the above graph does not contain an Euler circuit.

Example 2: In the following image, we have a graph with 6 nodes. Now we have to determine whether this graph contains an Euler circuit.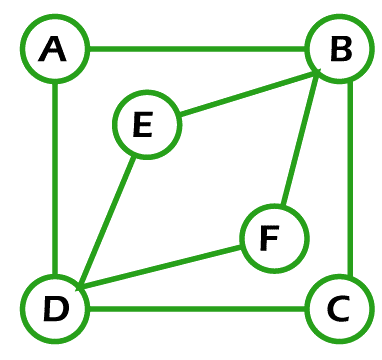

Solution:

The above graph will contain the Euler circuit if the starting vertex and end vertex are the same, and this graph visits each and every edge only once. The Euler circuit can contain the repeated vertex. So if we begin our path from vertex A and then go to vertices B, C, D, F, B, E, D and then A, in this process, the starting and end vertex are the same. The path (A, B, C, D, F, B, E, D, and A) also covers all the edges only once, and it does not contain any repeated vertex except the starting one. So the above graph contains an Euler circuit, which is described as follows:

Example 3: In the following image, we have a graph with 5 nodes. Now we have to determine whether this graph contains an Euler circuit.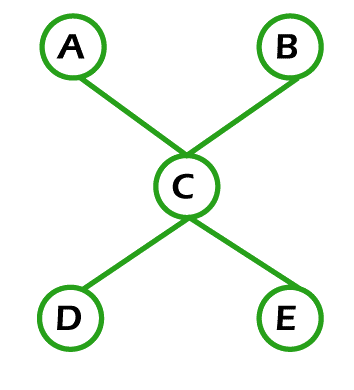

Solution:

The above graph will contain the Euler circuit if the starting vertex and end vertex are the same, and this graph visits each and every edge only once. The Euler circuit can contain the repeated vertex. If we begin our path from vertex A and then go to vertices C, D or C, E, then in this process, the condition of same start and end vertex is not satisfied, but another condition of covering all edges is not satisfied. This is because if we follow the path (A, C, D or A, C, E), many edges are repeated in this process, which violates the Euler circuit. So if we try to cover all the edges and vertices, the edges will be repeated. So the above graph does not contain an Euler circuit.

Semi Euler Graph

If there is a connected graph that does not have an Euler circuit, but it has an Euler trail, then that type of graph will be known as the semi-Euler graph. Any graph will be known as semi Euler graph if it satisfies two conditions, which are described as follows:

• For this, the graph must be connected
• This graph must contain an Euler trail

Example of Semi-Euler graph

In this example, we have a graph with 4 nodes. Now we have to determine whether this graph is a semi-Euler graph.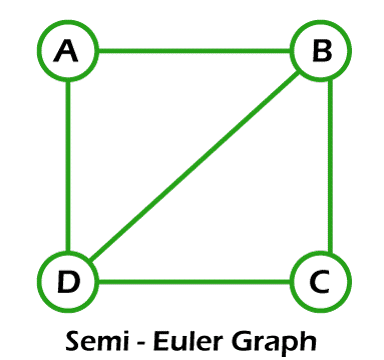

Solution:

Here,

• There is an Euler trail in this graph, i.e., BCDBAD.
• But there is no Euler circuit.
• Hence, this graph is a semi-Euler graph.

Important Notes:

When we learn the concept of Euler graph, then there are some points that we should keep in our minds, which are described as follows:

Note 1:

We have two ways through which we can check whether any graph is Euler or not. We can use any of the ways to do this, which are described as follows:

• If there is a connected graph with an Euler circuit, then that type of graph will be an Euler graph.
• If there is an even degree for all the vertices of the graph, then that type of graph will be an Euler graph.

Note 2:

We can use the following way through which we can check whether any graph has an Euler circuit:

• We will check whether all the vertices of a graph have an even degree.
• If it contains an even degree, then that type of graph will be an Euler circuit. Otherwise, it will not be an Euler circuit.

Note 3:

We can use the following way through which we can check whether any graph is a Semi Euler graph:

• We will check whether there is a connected graph that has an Euler circuit.
• If it is a connected graph and it has an Euler circuit, then that type of graph will be a Semi Euler Graph. Otherwise, it will not be a Semi Euler graph.

Note 4:

We can use the following way through which we can check whether any graph has an Euler trail:

• We will check whether more than two vertices of the graph contain the odd degree.
• If more than two vertices contain an odd degree, then that type of graph will be an Euler Trail. Otherwise, it will not be an Euler trail.

Note 5:

• If there is a connected graph, which contains an Euler circuit, then that graph will also contain an Euler trail.
• If there is a connected graph, which contains an Euler trail, then that graph may or may not have an Euler circuit.

Note 6:

• If there is an Euler graph, then that graph will surely be a Semi Euler graph.
• But it is compulsory that a semi-Euler graph is also an Euler graph.

Example of Euler Graph:

There are a lot of examples of the Euler graphs, and some of them are described as follows:

Example 1: In the following graph, we have 6 nodes. Now we have to determine whether this graph is an Euler graph.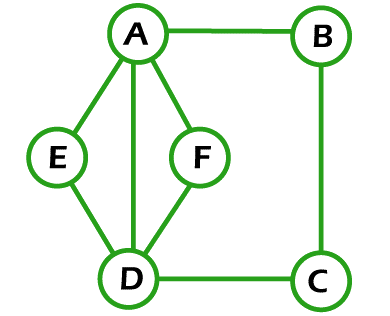

Solution:

If the above graph contains the Euler circuit, then it will be an Euler Graph. A graph will contain an Euler circuit if the starting vertex and end vertex are the same, and this graph visits each and every edge only once. So when we begin our path from vertex A and then go to vertices E, D, F, B, C, D and then A in this process, the starting and end vertex are the same. This path covers all the edges only once and contains the repeated vertex. So this graph contains the Euler circuit. Hence, it is an Euler Graph.

Example 2: In the following graph, we have 5 nodes. Now we have to determine whether this graph is an Euler graph.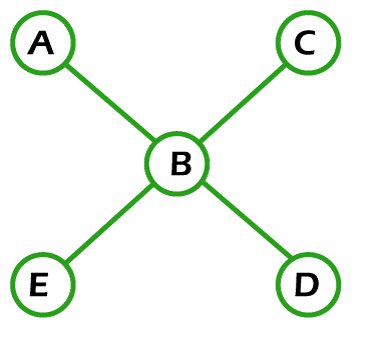

Solution:

If the above graph contains the Euler circuit, then it will be an Euler Graph. A graph will contain an Euler circuit if the starting vertex and end vertex are the same, and this graph visits each and every edge only once. So If we begin our path from vertex A and then go to vertices B, D or A, B, E, then in this process, the condition of same starting and end vertex is satisfied, but another condition of covered all edges only once is not satisfied. So when we follow the path (A, B, D or A, B, E), many edges are repeated in this process, which violates the definition of Euler circuit. So the above graph does not contain an Euler circuit. Hence, it is not an Euler Graph.

Example 3: In the following graph, we have 8 nodes. Now we have to determine whether this graph is an Euler graph.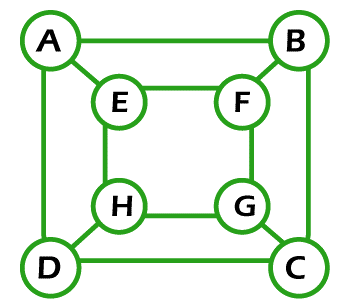

Solution:

If the above graph contains the Euler circuit, then it will be an Euler Graph. A graph will contain an Euler circuit if the starting vertex and end vertex are the same, and this graph visits each and every edge only once. So if we begin our path from vertex A and then go to vertices D, H, E, F, G, C, B and then A, then in this process, the condition of same starting and end vertex is satisfied, but another condition of covered all edges only once is not satisfied. So when we follow the path (A, D, H, E, F, G, C, B, A), in this process, many edges are not covered, i.e., A to E, G to H, F to B, and D to C, which violates the definition of Euler circuit. So the above graph does not contain an Euler circuit. Hence, it is not an Euler Graph.

Example 4: In the following graph, we have 7 nodes. Now we have to determine whether this graph is an Euler graph.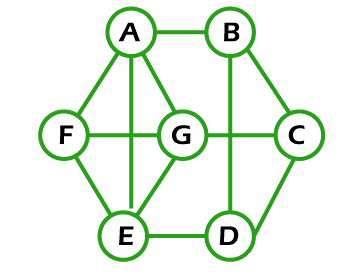

Solution:

If the above graph contains the Euler circuit, then it will be an Euler Graph. So if we begin our path from vertex A and then go to vertices F, E, G, C, D, B and then A, then in this process, the condition of same starting and end vertex is satisfied, but another condition of covered all edges only once is not satisfied. This is because the Euler circuit cannot repeat the edges. So when we follow the path (A, F, E, G, C, D, B, A), in this process, many edges are not covered, i.e., F to G, A to E, e to D, and B to C, which violates the definition of Euler circuit. So the above graph does not contain an Euler circuit. Hence, it is not an Euler Graph.

Example 5: In the following graph, we have 5 nodes. Now we have to determine whether this graph is an Euler graph.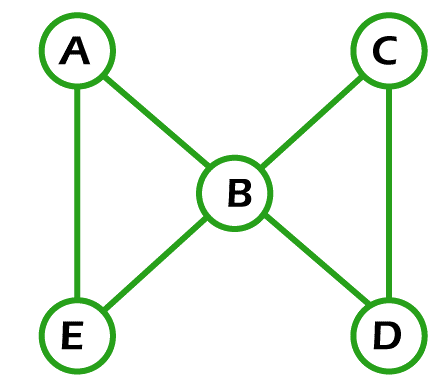

Solution:

If the above graph contains the Euler circuit, then it will be an Euler Graph. So when we begin our path from vertex A and then go to vertices B, C, D, B, E and then A, in this process, the starting and end vertex are the same. This path covers all the edges only once, and it contains the repeated vertex. So this graph contains the Euler circuit. Hence, it is an Euler Graph.

Example 6: In the following graph, we have 9 nodes. Now we have to determine whether this graph is an Euler graph.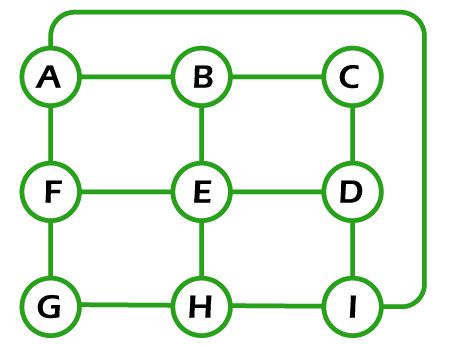

Solution:

If the above graph contains the Euler circuit, then it will be an Euler Graph. So if we begin our path from vertex A and then go to vertices B, C, D, E, F, G, H, I and then A, then the condition of same starting and end vertex is satisfied in this process, but another condition of covered all edges only once is not satisfied. So when we follow the path (A, B, C, D, E, F, G, H, I, A), in this process, one edge is not covered, i.e., A to F, which violates the definition of Euler circuit. So the above graph does not contain an Euler circuit. Hence, it is not an Euler Graph.