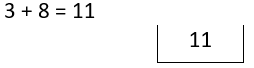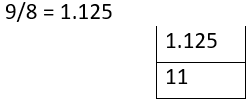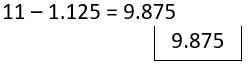Evaluation of a Postfix notation
Postfix notation:
The general mathematical way of representing algebraic expressions is to write the operator between operands: Example: a + b. Such representation is called the Infix representation. If we write the operator after the operands Example: a b +, it is called the Postfix representation. It is also called the "Reverse Polish notation".
Why Postfix?
Representing an algebraic expression in postfix eliminates parentheses and the need of precedence. The evaluation becomes simple. It is the ideal notation a computer uses to evaluate complex algebraic expressions using stacks. There are a lot of algorithms defined to convert an infix notation into postfix. This article explains the Dijkstra's algorithm and then we'll also see how to evaluate a postfix notation with Python codes for both conversion and evaluation.
Steps to convert infix to Postfix:
- Read the given expression from left to right. If the scanned element is an operand, simply append it to the resultant postfix expression.
- If the scanned operator is an operator and the stack is empty, push the operator into the stack
- If the scanned element is an operator and the precedence of the operator is greater than or equal to the precedence of the operator on the top of the stack, push it into the stack
- If the scanned operator is an operator and the precedence of the scanned operator is less than the precedence of the operator on the top of the stack, pop the operator on the top of the stack and add it to the postfix expression until the stack becomes empty or the precedence of the operator on the top of the stack is less than the precedence of the scanned operator. Now, push the scanned operator into the stack.
For example: 3 + 8 - 9 / 8
| Scanned element |
Stack |
Postfix notation |
| 3 |
- |
3 |
| + |
+ |
3 |
| 8 |
+ |
3 8 |
| - |
- |
3 8 + |
| 9 |
- |
3 8 + 9 |
| / |
-/ |
3 8 + 9 |
| 8 |
-/ |
3 8 + 9 8 |
|
Postfix expression: |
3 8 + 9 8 / - |
- Notice that the order of operands will stay unchanged, only the order of operators changes from an infix notation to postfix.
Python code:
Output:
Enter the infix notation separated by space: 3 + 8 - 9 / 8
38+98/-
Explanation:
- The user is prompted to enter an infix expression separated by spaces.
- The precedence() function is defined to assign a precedence level to each operator. Operators with higher precedence levels are evaluated first.
- The input expression is split into a list of tokens using the split() function.
- An empty string postfix and a list opstack are initialized.
- The program iterates through each token in the input list.
- If the token is an operator, the program checks the precedence level of the operator.
- If the operator has a higher precedence level than the previous operator in the opstack list, it is added to the opstack list.
- Otherwise, the previous operator is removed from the opstack list and added to the postfix string. This process continues until the operator can be added to the opstack list.
- If the token is a space, it is ignored.
- If the token is not an operator or a space, it is added to the postfix string.
- After all tokens have been processed, the remaining operators in the opstack list are added to the postfix string.
- The final postfix expression is printed to the console.
Evaluating a postfix expression:
Let us understand the concept using an example for clarity on stack operations.
Example:
Take the above converted postfix notation. First let us get the result from the infix notation:
3 + 8 - 9 / 8
= 3 + 8 - 1.125
= 11 - 1.125
= 9.875
- Order of evaluation: Scientific calculator (BODMAS)
Now, let us take the postfix expression we got from the previous conversion:
3 8 + 9 8 / -
- Read the expression from left to right, initialize a stack with the same length as the expression.
- If the element encountered is an operand, push it into the stack.
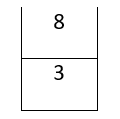
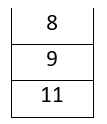
- If the element encountered is an operator, pop two operands a and b from the stack, apply the operator (b operator a) and push the result back into the stack.
- In the above example: 3 8 + 9 8 / -
Python program:
Output:
Enter the postfix expression: 3 8 + 9 8 / -
The result of the expression: 9.875
Explanation:
- The input expression is split into a list of tokens using the split() function.
- An empty list stack is initialized. The program iterates through each token in the input list.
- If the token is an operator, the program pops the top two values from the stack, performs the corresponding arithmetic operation, and pushes the result back onto the stack.
- If the token is a space, it is ignored.
- If the token is not an operator or a space, it is converted to an integer and pushed onto the stack.
- After all tokens have been processed, the final result is the only element left in the stack. This is printed to the console.
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now