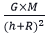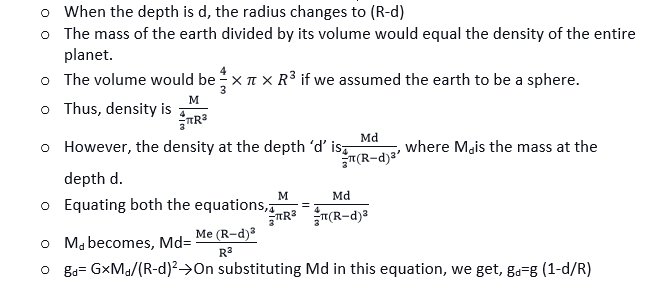Factors Affecting Acceleration due to Gravity

We've all played basketball, hurled a ball in the air, tried to catch it when it landed or witnessed fruit fall from a tree at some stage in our lives. These objects eventually touch the ground, as we witnessed with our own eyes. Have you ever questioned why it even occurs? In this section, we shall discover the physics that underlies these behaviours.

What is Acceleration?

• The pace at which an object alters its speed is termed acceleration. It might be slow or quick.
• Deceleration is the opposite of acceleration, which means slowing down.
• Let's use an illustration to understand better:
  • Imagine launching a stone into the atmosphere, then catching it when it lands.
  • When we throw a stone upward into the sky, we can see that as it ascends, its speed progressively reduces; therefore, we can say that the stone's acceleration diminishes (or decelerates). To rephrase it in another way, the stone is slowing down.
  • The speed slows until it drops to zero and stops momentarily after reaching a specific height before it begins to descend. Then it begins to crumble.
  • When it descends, we can see that the stone's speed rises as it gets closer to the ground. Thus, we can state that its acceleration is rising.
• We can extrapolate from this that acceleration is brought on by gravity. The speed of the stone kept rising as it began to fall as gravity drew it downward.
• Another illustration is that because of gravity; an orange tends to tumble to the ground when it separates from the tree. The orange is moving more quickly toward the surface, indicating that it is in an accelerated motion.
• Acceleration was evident in each of the previously considered situations because of gravity.

Let's find out what gravity is now.

What is Gravity?

• The fundamental concept of gravity that we perceive is that it is a force that the earth uses to drive objects towards it or that it is something that pushes an object towards the earth.
• Isaac Newton is credited with introducing the notion of gravity in the 1680s in his work Principia, which also contained the general rule of gravitation.
• He was seated beside an apple tree, according to folklore. He wondered what had brought the apple to the ground as it dropped on his head.
• Newton believed that objects other than apples, such as the sun, moon, and planets, were also affected by gravity.
• You may have also seen that when you jump into the air, either when you are playing or when you are excited, you are all back on the ground after a short period. This is caused by gravity.
• How, then, does the earth draw things toward it?
  • The force of attraction between any two masses in the cosmos is driven by the gravitational force.
  • To comprehend this, consider any two objects with non-zero mass, such as planetary bodies, people, animals, etc.,both items will make an effort to draw one another nearer them.
• The attractive force between a pair of objects with non-zero mass separated by a distance is known as gravitational force.
• The earth employs additional forces in conjugation with gravitational force to draw things towards it.
• Every mass-containing body experiences a gravitational pull or force from every other mass-containing entity.
• The mass of the objects affects how strong the pull is.
• The earth is one object, and people are the other object. Each of these items pulls the other into itself when it comes to the earth and humans. And gravity is something that enables this to happen.
• Moons are orbiting planets, planets orbiting stars, and stars held in galaxies wouldn't exist without gravity.
• Because of the moon's gravitational influence, ocean and sea tides occur.

Acceleration due to Gravity

• As we previously observed, when we threw a stone, its speed dropped as it rose before abruptly ceasing for a brief period. The stone then began to tumble down.
• Additionally, we noticed that the stone's speed was rising.
• Acceleration resulted from this shift in velocity and direction.
• This acceleration was brought on by the gravitational force.
• All freely falling objects experience acceleration due to gravity, which is referred to as acceleration due to gravity.
• The stone would have continued to move in the direction it was launched if gravity and air resistance did not exist.
• Free fall is the term employed to describe when an object descends toward the earth's surface due to the earth's gravitational pull.
• When objects are tossed from a specific height, it was once believed that lighter bodies fall more gradually and heavier bodies travel faster.
• If a feather and a metal penny are thrown from the exact height concurrently, the metal penny will touch the ground first, and the feather will reach afterward.
• Galileo, however, was the one who demonstrated that objects of differing weights and sizes could be dropped concurrently from the same elevation and would all hit the ground at the same moment through his studies carried out from the Leaning Tower of Pisa. In other words, when anything is dropped from a particular height, it accelerates evenly due to the earth's attraction, regardless of the body's mass.
• As a result, we can redefine acceleration due to gravity as the consistent acceleration brought about by the earth's gravitational force on freely falling objects.
• The symbol g symbolizes the acceleration caused by gravity, which fluctuates based on the celestial body.
• For instance, the acceleration brought on by gravity will indeed fluctuate on the moon from the earth. On Jupiter and Pluto, the acceleration caused by gravity would have different values.
• The unit of acceleration caused by gravity is equivalent to the unit of acceleration, which is m/s².

Derivation of formula

• We know that the acceleration caused by gravity, or g, on or near the planet's surface is 9.81 m/s². But first, let's examine how we came to this conclusion.
• Two alternative formulae can determine an object's weight on the planet.
• One is by applying Newton's second rule of motion.
  • It claims that mass times acceleration equals force or F=ma.
  • However, in a free fall, force, or the force of gravity, is defined as the combination of mass and acceleration due to gravity.
  • Thus, F=mg.
• And the second is by applying newton's law of universal gravitation, which states that the force of gravity between pair of objects is equivalent to the gravitational constant G multiplied by the mass of one object (such as the earth) multiplied by the mass of any other object, fractionated by the square of the interspace between the two objects.
  • F=G×M×m/d²
  • G is the universal gravitational constant in this equation.
  • The mass of the earth is M.
  • m is the object's mass.
  • The symbol d gives the two-object distance.
• Since the two equations above are similar, we may state that the universal law of gravitation and Newton's second law are equivalent: mg= G×M×m/d².
• We can eliminate m because it appears on both aspects of the equation. All that is left is the formula for calculating gravity, which is g= G×M/d².
• Since we are determining the acceleration due to gravity for objects near or on the surface, d is equivalent to the radius of the planet R, so the equation becomes g=GM/R².
  • G is equal to 6.67.10-11Nm²/kg² in this situation.
  • 97.1024 kg equals M
  • The earth's radius, R, measures 6.371.106 meters.
• By rearranging all of these numbers in the formula above, g = 9.81 m/s².

Note:

• As either or both of the masses of the objects increase, the force rises, and it falls as the square of the space between them widens.
• For instance, the force of gravity is increased by doubling the mass of one of the objects. But when the distance between the items is doubled, just one-quarter of the initial force is created.
• Only an attracting force, gravity, has a weaker effect at a distance.
• The gravitational influence between the earth and the sun keeps the planet in its orbit.
  The earth would keep moving straight forward without this force.

Factors affecting acceleration due to gravity

1. The Shape of the Earth

• The formula for the acceleration caused by gravity is g = G×M/R².
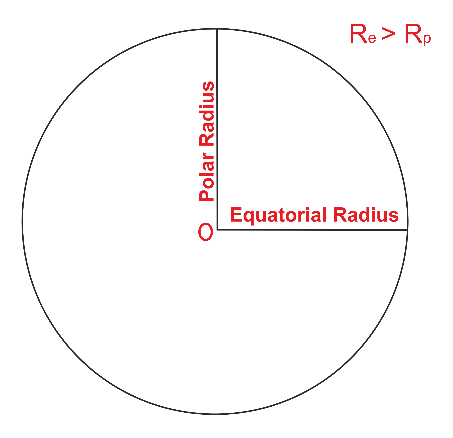
• We are aware that the planet is a geoid rather than round.
• Geoid refers to a structure flattened at the poles and bulging toward the equator.
• Equatorial radius (Re), also known as the planet's radius near the equator, is larger than the polar radius, which is the planet's radius near the poles (Rp). Consequently, Re>Rp.
• This is because the equator is longer than the poles since it has moved more than the poles have (and hence is bulged).
• The radius of the planet 'R' and the acceleration caused by gravity 'g' is inversely related to one another, according to the equation for gravitational acceleration.
• As a result, gravity will be stronger near the poles, where the radius value is lower.
• However, gravity will have a lower effect on the equator because of its greater radius.

2. Altitude or Height

• The formula for the acceleration caused by gravity is g = G×M/R².
• This equation is valid when we assume an entity to be adjacent to or on the planet's surface.
• But what if the object is located at a particular height or altitude above the earth?
• Let's investigate how this situation will affect the value of gravitational acceleration.
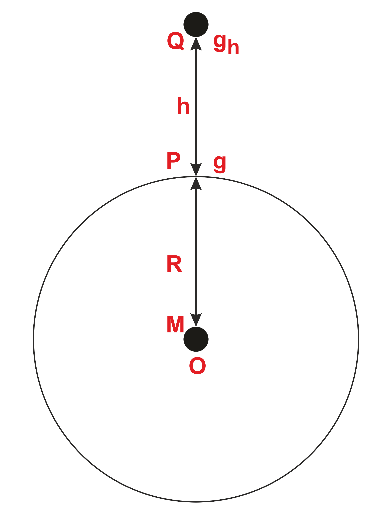
• Assume that an object is located at a distance 'h' from the planet's surface.
  • The formula is completed by adding the radius and this height, or elevation, h.
  • Now, g =
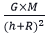
• The numerator, which symbolizes the value of the acceleration caused by gravity, now declines as the denominator rises.
• From this, we can infer that gravity's value will diminish as elevation or altitude rises.
• Mathematically, this can be expressed as:
  
• When height exceeds the earth's radius, we might employ this formula. Meaning when h>>R.
• When height is less than the earth's radius, h<<r, g_h=g(1+h/R)^-2

3. Depth or Center of the Earth

• The acceleration caused by gravity 'g' is given by: g=G×M/R².
• This equation still holds if an entity is adjacent to or on the planet's surface.
• But what if the entity is positioned at a particular distance under the earth?
• Let's investigate how gravity will change in this case.
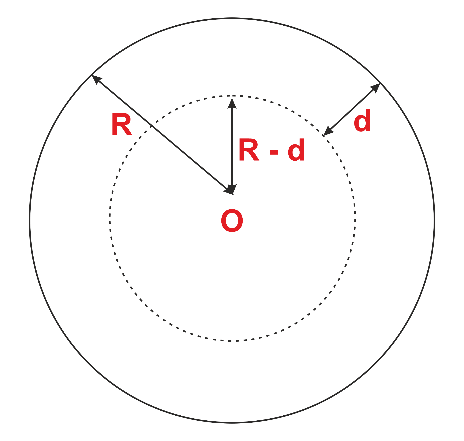
• Assume that an object is located a specific distance (d) below the earth's surface.
• The radius is almost insignificant when the object is at the earth's center.
• The radius will shrink as we reach the earth's center. Similar to how the object's mass is minimal when it reaches the earth's center.
• As a result, the acceleration caused by gravity becomes zero in the earth's core.
• The same can be expressed mathematically as g = G×M/R².
  

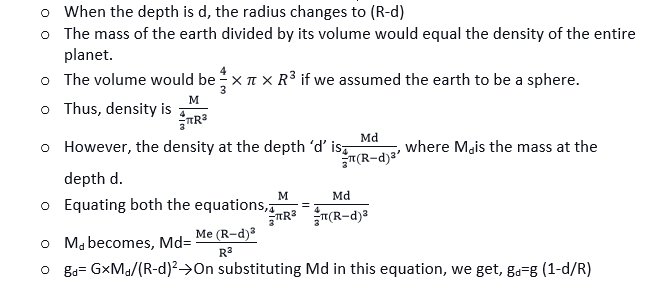
Practice Questions

1. What is acceleration?

The pace at which an object alters its speed is termed acceleration.

2. What is acceleration due to gravity?

The constant acceleration caused by the earth's gravitational pull on freely falling objects is known as acceleration due to gravity.

3. What elements influence the acceleration brought on by gravity?

• The earth's shape.
• Earth's rotational movement.
• Height above the surface of the earth.
• Depth under the surface of the earth.

4. Describe how the earth's form affects the rate at which gravity accelerates objects.

The extent of the equator is greater than the extent of the poles because the equator bulges and the poles are flatter. Or, to put it another way, the polar radius is smaller than the equatorial radius.Since the relationship between radius and gravity is inverse, the greater gravity will be found near the poles where the radius is less. Similarly, gravity has a lower value at the equator when the radius is greater.

5. Describe how the earth's and the object's mass have no bearing on the amount of acceleration caused by gravity.

g=GM/R2 is the formula for the acceleration caused by gravity.According to our analysis, this calculation considers the entity's mass. Consequently, we can state that the value of gravity is regardless of an object's mass.Observe that the earth's mass stays unchanged when an entity is thought to exist on the planet's surface. Or, to put it another way, the strength of gravity is independent of the mass of the earth.