Find Rectangle in a Matrix with Corner as 1 in Java

In this section, we are going to solve another popular coding problem that was asked by e-commerce companies Flipkart and Amazon. Also, we will solve the problem with different approaches and create Java programs.

Problem Statement

In a boolean matrix of size m*n, we need to find if there exists a rectangle or square in the matrix whose all corners are equal to 1. If we found corners of a rectangle or square as 1, return true, else return false. For example, consider the following matrix.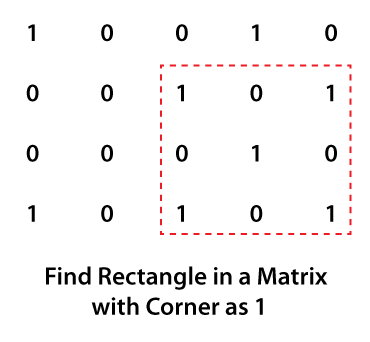

Solutions to the Problem

The problem can be solved by using the following approaches:

• Brute Force Approach
• Optimized and Efficient Approach

Brute Force Approach

It is a naive approach to solve the problem. In this approach, first, we iterate over rows and columns of the matrix with the help of two for loops, one for rows and the other for columns. It iterates over each element of the matrix one by one.

If we found an element as 1, which means matrix[i][j]==1, we have to search for another 1 in the same row (i-th) but in another column (j2-th), and in the same column (j) but in another row (i2). Besides this, we have to search for another corner as 1 (i2, j2).

Therefore, for searching 1 as a corner, we need to run two for loops, one for a row and the other for a column.

Also, we need to check all the corners are 1 or not.

Let's write the algorithm for the above approach.

Algorithm

Let's implement the above approach in a Java program.

MatrixRectangle1.java

Output:

The given matrix forms a rectangle with 1 as the corner.

Complexity

In the above approach, we have used four for loops two for rows, and two for columns, so the time complexity will be m*n*m*n i.e. O(m² * n²).

Optimized and Efficient Approach

The approach provides the optimized solution for the problem. In this approach, we start scanning the matrix from the first element and keep scanning rows one by one. If we found a pair of 1's in the same row, store the corresponding index value in the HashSet. The following figure depicts the same.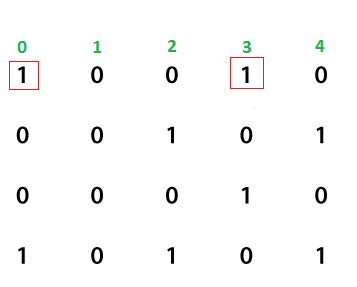

As we can see in the above matrix, the first row contains a pair of 1's whose index value is (0, 3). Similarly, we will scan for the second row and found a pair of 1's at index (2, 4).

We have to repeat this process for each row.

Here a question arises, what if there are more than 1's in the same row (consider the last row of the matrix). For this, we need to run another for loop. In the last row, there exists more than one pair of 1's i.e. (0, 2), (0, 4), and (2, 4).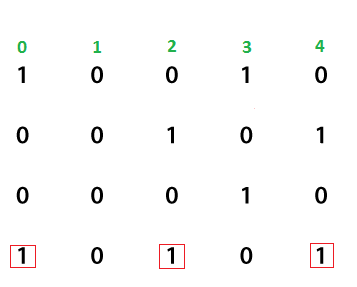

We observe that a pair of 1's at position (2, 4) is already stored in the Set, we found another pair of 1's in the same columns, it means it forms a rectangle or square.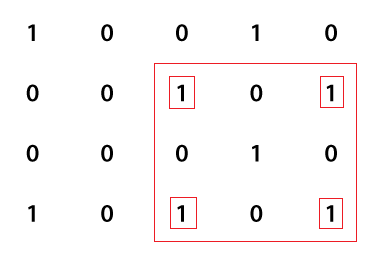

The above approach can understand in easy steps, as follows:

1. Iterate over the matrix in the top to down fashion, line by line.
2. For each line, store each combination of 1's and push that combination into a HashSet.
3. If we found that combination again in the same line, we get a rectangle or square.

Let's implement the above approach in a Java program.

MatrixRectangle2.java

Output:

The given matrix forms a rectangle with 1 as the corner.

Complexity

In the above approach, we have used three for loops two for rows, and one for columns. So, the time complexity for the above approach will be m*n*m i.e. O(m² * n). We observe that the time complexity is optimized in comparison to the brute force approach.