First Order Reaction

A form of chemical reaction known as a first-order reaction occurs when the concentration of just one of the reactants directly affects the reaction's rate. Biochemistry, pharmacology, and environmental science are a few of the chemistry disciplines where these processes are frequently seen. The definition, traits, kinetics, and applications of first-order reactions, as well as other important topics, are covered below:

Definition of First-Order Reaction:

A first-order reaction is a chemical reaction in which one of the reactants' quantity directly affects how quickly the reaction proceeds. This reaction law can be written numerically as:

Rate = -d[A]/dt = k[A]¹ = k[A]

Where [A] is the concentration of the reactant A, and k is the rate constant of the reaction. Since the reaction has an order of 1 with regard to A, it is referred to as a first-order reaction. Since there is only one reactant participating in the reaction, the reaction's overall order is also 1. Some examples of First-Order Reactions:

• SO₂Cl₂→ Cl₂ + SO₂
• 2N₂O₅ → O₂ + 4NO₂
• 2H₂O₂ → 2H₂O + O₂

Graphical Representation of First-order Reaction

A first-order reaction is graphically represented by a depiction of the natural logarithm of the reactant concentration ([A]) versus time (t). An "ln[A] versus t" plot, also known as an "ln[A] versus time" plot, is what this plot is.

The plot depicts an exponential decline in reactant concentration over time after starting with a high concentration at time zero. As the concentration of the reactant declines over time, the slope of the plot, which is negative, also gets steeper. The time it takes for the reactant concentration to drop to half its initial value can be used to determine the reaction's half-life from this plot.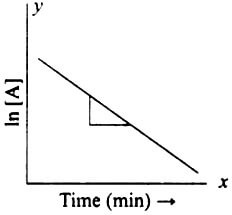

Characteristics of First-Order Reaction:

First-order reactions differ from other kinds of reactions in that they display a few distinctive traits. Some examples of these qualities are:

• The reaction's half-life is constant and unaffected by the reactant's starting concentration.
• With time, the reaction rate falls off rapidly.
• The rate constant is independent of the initial concentration of the reactant.
• The rate of the reaction is proportional to the square of the reactant concentration.
• The square root of the reactant concentration determines the rate of the reaction.
• The rate of reaction is proportional to the reactant's concentration's natural logarithm.
• The concentration of the reactant and the rate of the reaction directly correlates.
• The rate of the reaction also increases by four times when the concentration of A is four times higher. In general, the rate of the reaction increases by n times for every n-fold increase in reactant concentration.

Kinetics of First-Order Reaction:

The above-mentioned rate law equation can be used to describe the kinetics of first-order reactions. This equation shows that the rate of the reaction is directly proportional to the concentration of the reactant. As the concentration of the reactant decreases with time, the rate of the reaction also decreases. The rate constant k is a measure of the intrinsic reactivity of the reactant and is independent of the initial concentration of the reactant.

The integrated rate law for a first-order reaction can be derived from the rate law equation. This equation relates the concentration of the reactant at any time t to its initial concentration [A_O] and the rate constant k.

ln [A_t] - ln [A_O] = -kt

Where [A_t] represents the reactant concentration at time t, [A_o] represents the reactant concentration at the start of the reaction, k represents the rate constant, and ln represents the natural logarithm function. This equation shows that the concentration of the reactant decreases exponentially with time and that the half-life of the reaction is constant and independent of the initial concentration of the reactant.

Pseudo First-order Reaction

Pseudo-first-order reactions are ones that are not first-order but an approach or seem to be first-order because the reactant(s) is/are present at higher concentrations than other reactants. The rate law expression's product of the powers of the reactant concentrations may be used to describe the order of a chemical reaction. First-order, second-order, pseudo-first-order, etc. reactions may be categorized based on the concentration of the reactants. It may be difficult to comprehend a second-order reaction since it involves simultaneous measurement of both of its reactants.

Further difficulties might arise because, for instance, exact concentrations of each reactant are necessary in order to determine the reaction rate. If one or both of the necessary reactants are costly, the experiment might end up costing a lot of money. To avoid more complicated, costly calculations and experiments, we may use the pseudo-1st-order reaction, which involves treating a 2nd order reaction as a 1st order reaction.

Half-Life

The half-life of a first-order reaction is the time it takes for the concentration of reactant A to decrease to half of its initial value. The half-life is a characteristic property of the reaction and is independent of the initial concentration of A. The half-life of a first-order reaction can be calculated using the integrated rate law equation:

ln([A]/[A_o]) = -kt

A is initially concentrated at [A_o], [A] is the concentration at any moment t, k is the rate constant, and t is the passage of time. To solve for t, we obtain:

At half life period,

t= t_1/2 and [A] = [A]/02

On substituting,

k = 1/ t_1/2 . log_e {[A_o] /( [A_o] / 2)}

t1/2 = 0.693/k

This equation demonstrates how the relationship between the rate constant and the half-life of a first-order process. A shorter half-life and a quicker response result from a higher rate constant.

Applications of First-Order Reaction:

There are numerous uses for first-order processes in the fields of chemistry, biochemistry, pharmacology, and environmental science. These are a few of the applications:

1. Radioactive Decay:

There is a first-order process that occurs after radioactive isotopes decay. The half-life of the decay is constant, and the rate of decay is proportional to the quantity of radioactive nuclei present at any given moment.

2. Enzyme Kinetics:

It is common for enzyme-catalyzed processes to have first-order kinetics. The rate of the reaction falls off rapidly over time and is inversely related to the enzyme concentration.

3. Pharmacokinetics:

Drug removal from the organism is governed by first-order kinetics. The rate of elimination is exactly proportional to the drug concentration in the body, and the half-life of the elimination is constant.

4. Chemical reactions in the environment:

Pollutants in the atmosphere frequently degrade according to first-order kinetics. The half-life of degradation is constant, and the rate of degradation is proportionate to the pollutant's concentration.

Exponential Decay

In a first-order reaction, the concentration of reactant A drops exponentially over time. This implies that the reaction rate falls off rapidly over time. The concentration of A at any moment t can be determined using the integrated rate law equation:

[A]t = [A_o]e^-kt

Where k is the rate constant, e is the base of the natural logarithm, [A]t is the concentration of A at time t, and [A_o] is the starting concentration of A. Experimentally, by monitoring the concentration of A over time, the exponential decline in A's concentration can be seen.

Temperature Dependence:

The rate constant and response rate both rise with increasing temperature. The Arrhenius equation can be used to explain this relationship:

k = Ae^(-Ea/RT)

k is the rate constant, a pre-exponential component is known as A, the activation energy is known as Ea, the gas constant is known as R, and the temperature is known as T in Kelvin. This solution demonstrates that as the temperature rises, the rate constant grows exponentially, increasing the rate of the reaction.

Conclusion

Concentration dependence, exponential decay, half-life, rate constant, and temperature dependence are just a few of the distinctive characteristics of first-order processes. These characteristics can be used to describe and forecast how first-order responses will behave in various scenarios.